PIC AVR 工作室->TopPage->オペアンプ入門->もう一歩
もう一歩 …演算と増幅の回路の計算…
オペアンプを使った代表的な演算回路、増幅回路について、動作の仕組みと設計上の計算を理解していきたいと思います。
色々な応用回路について
まずは、オペアンプの応用回路について列挙して、概要だけ簡単に触れておきます。
増幅回路と演算回路には元々境界線があるわけではありませんが、なんとなく便宜上分けたいので、 増幅回路、演算回路、その他、とおよそ3つに大別して考えることにします。
増幅回路
| 回路 | 用途、動作 |
|---|---|
| 反転増幅 | 入力電圧を正負反転し、固定倍の増幅率で増幅して出力する。 |
| 非反転増幅 | 入力電圧を正負そのままで、固定倍の増幅率で増幅して出力する。 |
| ボルテージフォロア | 非反転増幅の特殊な例で、帰還抵抗を0Ω(出力と反転入力を直結)とし、倍率を1倍固定にする。 出力インピーダンスを小さく出来る。 |
- 表中のリンクをクリックすると、ページ内の解説部分に移動します。 -
演算回路
| 回路 | 用途、動作 |
|---|---|
| 加算回路 | 2~5個程度の入力端子の電圧値を加算して出力する。ただし反転増幅の応用なので、正負反転して出力される。 |
| 減算回路(差動増幅回路) | 2つの入力の電圧差を取って出力する。(反転増幅と非反転増幅の組み合わせ回路) |
| 加減算回路 | オペアンプが2個必要。上記の加算回路2つを直列に繋げ、1段目の入力を正値、2段目を負値とみなし、 各入力を足し引きして出力する。(1段目はマイナスを2回掛けることになるので正値になる) |
| 対数増幅回路 | 入力電圧の”対数関数”を取って出力する回路。 |
| 逆対数増幅回路 | 対数の逆関数…つまり入力電圧の”指数関数”を取って出力する回路。 |
| もう一つの加減算回路 | 上記の加減算回路と動作は似ているが、つくり的には減算回路(差動増幅回路)に似ていて オペアンプは1個だけでOKという回路。使用するオペアンプが少ないので安く済む代わり、抵抗計算はメチャメチャ大変…。 |
- 表中のリンクをクリックすると、ページ内の解説部分に移動します。 -
その他の回路
| 回路 | 用途、動作 |
|---|---|
| シュミット回路 | いわゆる、シュミットトリガ回路のようにスレショールドが得られる回路。負帰還ではなく、正帰還を掛ける。 |
| リミッタ回路 | 出力電圧の範囲が、正負ある程度以上にならないように制限をかける回路。 |
| ローパスフィルター | ある程度以上の周波数をカットして、それより低い周波数だけ通す回路。 ただのCRフィルタと違って、出力インピーダンスが小さい。 |
| ハイパスフィルター | ある程度以下の周波数をカットして、それより高い周波数だけ通す回路。 ただのCRフィルタと違って、出力インピーダンスが小さい。 |
| バンドパスフィルター | あるバンド幅の周波数だけを通して、それ以外の周波数をカットする回路。 通過させるバンドの幅によって何通りか存在。簡単なのは、ハイパスフィルターとローパスフィルターを 直列にする方法で、バンド幅が広く出来る。 |
| インスツルメンテーションアンプ | オペアンプ3つで構成。入力インピーダンスが高い。 外部から進入する同相ノイズに強いアンプ。 |
| アナログメモリ | 一般に、サンプルホールドやピークホールドと呼ばれるモノ。コンデンサに一時的に電気を溜め込んで、 そのコンデンサの電圧をボルテージフォロアで出力する。 |
その他の情報について
この他にも色々な回路があるのですが、端折ります。ご興味のある方は、 絵ときでわかる オペアンプ回路とか、 東北学院大学のページ とか、京都大学のページ とかをごらん頂くとよろしいかと思います。
マイコンとの接続によく使う回路
マイコンと組み合わせて使うような回路
一応マイコン関係のサイト(?)ですので、上記の中からマイコンと繋いで使うことが多そうな応用回路について 触れていきたいと思います。取り上げる回路は私の独断と偏見で選択しました。
ひとまず「反転増幅回路」「非反転増幅回路」「ボルテージフォロア」「加算回路」「減算回路」「加減算回路(両々とも)」を 取り上げることにします。あとは気が向いたら追記していくことにします。
まぁ、おおよそ絵ときでわかる オペアンプ回路で理解した内容 がメインなので、正確な情報はそちらを見ていただいたほうが早いかもしれません。
反転増幅回路
特徴
2つの外付け抵抗を使って、その抵抗値を”てこ”のアームにして使用し、てこの原理で増幅をします。入力が増加すると 出力が減少するという具合に、入出力が反転動作をするので反転増幅回路と呼ばれます。
2つの抵抗値の比率で簡単に増幅率が設定出来ます。オペアンプによる増幅回路といえばまず真っ先に挙がるのがこれという代物ですので、 まずはこの回路についてどんな風に回路が働くのか、どうして計算式がこうなるのかを理解してみてください。これ1つ理解できれば、 他の回路もたいして難しくはないかと思います。
回路図と計算式
オペアンプの理想条件の一つに「入力インピーダンスは無限大」というのがあったかと思いますが、この特性のために反転入力端子に 流れ込む電流は0になります。そうすると、R1とR2に流れる電流はともに等しくなります。
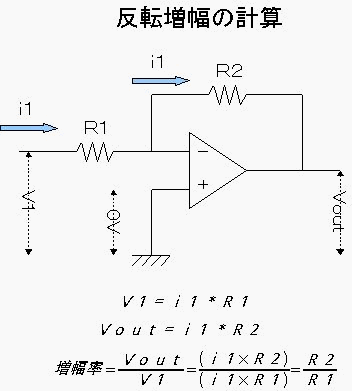
R1、R2に流れる電流をともにi1と置くと、反転入力に与えられる電圧V1とR1の関係はオームの法則から上図のとおり表されます。 同様に出力電圧VoutとR2の関係も上図のように表すことが出来ます。
このときの電圧の増幅率は、VoutをV1で割った値なので、計算するとR2/R1となることが判ります。 これが、増幅率が抵抗値の単純な比率で設定出来るという理由です。
ただし、非反転入力端子がグランド電位に固定された状態で負帰還がかかって、かつ反転入力端子もバーチャルショート (バーチャルグランド)によって0Vのため、反転入力端子が常に0V固定の”てこの支点”となります。よって、入力電圧と出力電圧は 正負が逆転した値となります。(という意味では、増幅率は「-R2/R1」と符号をつけて表した方が解りやすいですね)
使用上の注意
抵抗の比率を大きく取れば、いくらでも増幅率を増大させることが出来ると思ってしまうのですが、現実には限界があります。
理想的なオペアンプは、オフセットはゼロ、温度ドリフトもゼロ、ノイズも生じないのですが、現実のオペアンプには オフセットも温度ドリフトも有るし、ノイズも生じます。あまり大きな増幅率を設定すると、これらの攪乱要因まで一緒に 増幅してしまい、一体何を増幅したのかがわからなくなってしまいます。
そのため、あまり大きな増幅率は設定できません。現実的には、大きくても100倍~200倍程度に抑えておくほうが安全 というお話です。(絵ときでわかる オペアンプ回路P41より)
また、R1、R2に流す電流は、大きすぎれば抵抗の発熱によるドリフトが発生したり、消費電力が大きくなったりしますし、 小さすぎるとノイズに弱い回路になります。一般には、1kΩ~100kΩの中に留めておくとよいようです。
なお当然ですが、R1>R2に設定すれば、増幅率を1倍より小さい値にすることも可能です。
例
増幅率が10倍の反転増幅回路を作ってみることを考えてみます。
R1、R2ともに1kΩ~100kΩに入る値で考えるので、R1を1kΩ、R2を10kΩとすると丁度10倍に設定できます。
この回路で入力端子に0.5Vを入力すれば出力は-5V。-0.3Vを入力すれば3Vが出力されることになります。
クリックするとページの上部に戻ります。非反転増幅回路
特徴
2つの外付け抵抗を”てこ”のアームに利用するという点では反転増幅回路と一緒です。ただ、下図のように配線のつなぎ方が異なります。 入力と出力の増減方向が同じなので、非反転増幅回路と呼ばれます。
回路図と計算式
入力信号を非反転入力に繋いで使います。そしてR1はグランドと反転入力の間に、R2は”帰還抵抗”として反転入力 と出力端子の間に繋ぎます。
例によって「入力インピーダンスは無限大」なので反転入力端子に流れ込む電流はゼロ。そして反転入力端子は非反転入力端子と バーチャルショートで同電位(両方とも電圧はV1)。よって、R1の左端が支点(=0V)、R1とR2の間が力点(電圧=V1)、 R2の右端つまり出力端子が作用点(増幅後の電圧=Vout)となります。
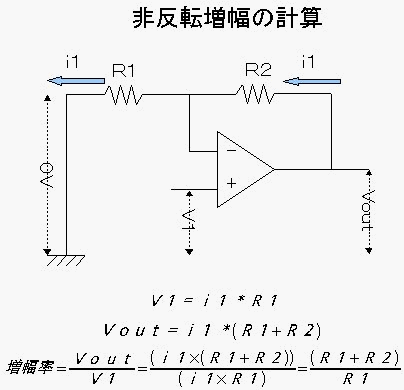
例によってR1、R2に流れる電流をともにi1と置いて考えます。(非反転増幅は単電源で使用することが多く、出力電圧も 入力信号もプラス電圧であることが多いので、電流の向きは右から左で描いてみましたが、便宜上の話なのでどっちでもいいです)
非反転入力に与えられる電圧(=反転入力の電圧)V1とR1の関係はオームの法則から上図のとおり表されます。 そして出力電圧Voutですが、支点が左端にあるので出力電圧Voutは(R1+R2)両方の抵抗にかかる電圧となります。 よって、計算式は上図のとおりとなります。
電圧の増幅率はやはりVoutをV1で割った値ですが、計算すると(R1+R2)/R1となることが判ります。 2つの抵抗で増幅率が設定できると言う点では反転増幅と似ていますが、計算式の形がちょっと異なりますね。
使用上の注意
反転増幅回路と同様に、抵抗の比率をべらぼうに大きく出来るわけではなく、実用上は限界があります。
あまり大きな増幅率は設定できません。現実的には、やはり大きくても100倍~200倍程度に抑えておくほうが安全 というお話です。また、抵抗値は一般には1kΩ~100kΩを選択するとよいようです。
また、計算式をご覧頂くとおわかりいただけると思いますが、分子は必ず分母より大きくなるので、増幅率は1倍より 大きい値にしか設定できません。1倍より小さい増幅率を使いたい場合は、反転増幅回路を使わないと実現できません。 その場合は当然負電源が必要になります。念のため…。
まぁ、1倍より小さい増幅率を実現する手が無いわけでも有りません。…単に入力段階で抵抗の分圧を行うという 方法になりますが。でもそれは非反転増幅回路と切り離して考える方が自然だと思うので、分圧は分圧、非反転増幅は非反転増幅 と分けて解説いたしました。設計上も、その方が間違えが無いだろうと思いますし。
例
増幅率が10倍の非反転増幅回路を作ってみることを考えてみます。
R1、R2ともに1kΩ~100kΩに入る値で考えるとして、R1を1kΩ、R2を9kΩとすると (1+9)÷1=10で丁度10倍に設定できます。
この回路で入力端子に0.5Vを入力すれば出力は5V。-0.3Vを入力すれば-3Vが出力されることになります。
(もちろん、正負の電圧を扱う時には正負両方の電源が必要です。正電圧の単電源なら正電圧だけ、 負電圧の単電源なら負電圧しか扱えません。)
クリックするとページの上部に戻ります。ボルテージフォロア
特徴
入力信号を非反転入力につなぎ、出力端子を反転入力に直接繋いで帰還をかけて使う方法です。非反転増幅回路の 抵抗を取っ払った形です。
(スペルから言うとボルテージフォロワの方がしっくり来るでしょうか)
回路図と計算式
入力が正なら出力も正、負なら負と、出力される電圧は入力信号と同相で取り出せます。非反転出力と同様です。 出力電圧の値は入力電圧と等しくなります。
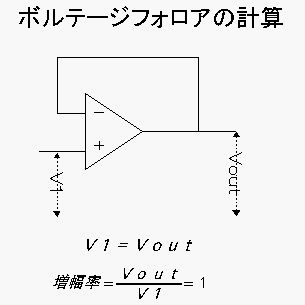
入力電圧=出力電圧となるので、増幅率は常に1です。「じゃぁ意味無いじゃん!」と思うなかれ。ちゃーんと意味があります。
入力信号側のインピーダンスが大きくても、ボルテージフォロアを通せばインピーダンスを小さくすることが出来ます。 つまりインピーダンス変換の為に使われます。また、入力側と出力側の回路を分離することができ、出力側の回路が入力側の 回路に対して影響を及ぼすことを防げます。(フォトインタラプタのように絶縁するということでは有りません。念のため。)
使用上の注意
非反転増幅回路のところで触れましたが、帰還抵抗は1kΩ~100kΩ程度に収めることで安定した増幅が 出来るのですが、ボルテージフォロアの場合は回路図をご覧になると判るように帰還抵抗=0Ωです。
非反転増幅回路の2つの抵抗を、R1=無限大、R2=0とした特殊ケースと考えることが出来ますね。
オペアンプ君にとってはとても辛い回路です。発振しやすくなります。オペアンプによってはボルテージフォロアで 使用出来ないものもあります。詳しくはデータシートをご覧ください。
そういえば、以前ボルテージフォロアを使ってビデオ信号を扱う実験をした際、 たしかにLM7171は発振してたっけなぁ…。
例
マイコンの出力をDA変換する方法の一つとして、抵抗を沢山使ったR2Rラダーというのがあります。 (R2Rについては解説を省くので、詳しいことは検索かけてみてください)
R2RのDA変換回路の出力は、抵抗群がそのまま出力インピーダンスとなるわけで、大きな電流を取り出すことが出来ません。
こういうときに、R2Rの出力をボルテージフォロアに繋げば、出力インピーダンスはオペアンプの出力インピーダンスそのまま に変換することができるわけです。
また、R2Rの抵抗群と後続の回路を分離しておかないと、後続回路とR2R回路が混ざって変な風になってしまうのですが、 ボルテージフォロアを通すことによってR2R抵抗の計算を独立して行うことが出来ます。
クリックするとページの上部に戻ります。加算回路
特徴
2つ以上の入力電圧を合計した電圧を出力する回路です。
反転増幅回路の応用で、形状的には反転増幅回路の入力側が複数に増えた形です。反転増幅の応用なので出力結果は 反転されて出力されます。(例えば、1V+2V=-3Vのようになります) 正負反転して出力されるので、 反転加算回路とも呼ばれます。
入力が複数になるので反転増幅回路のような”シーソーの絵”に単純化することは出来ないのですが、計算の仕方は ほぼ同じ考え方です。オームの法則がわかれば簡単に計算式が導き出せます。
回路図と計算式
ひとまず、入力電圧が3つの場合を例にとってみます。基本的には入力が幾つでも考え方は一緒です。5~6入力程度までは 実用上問題なく使えるようです。
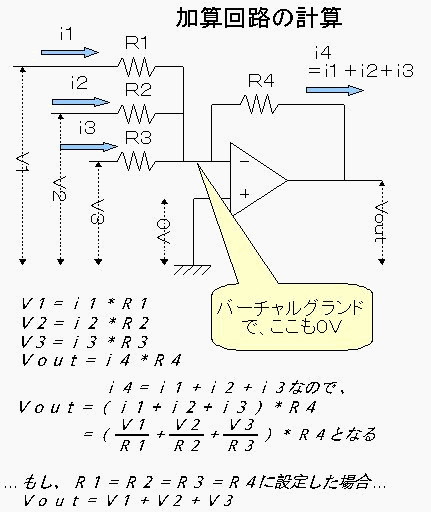
本当は、計算式には符号もつけて表した方がいいのでしょうが、簡略化のために符号を取っ払いました。
まず、反転入力端子の電圧について。非反転入力端子がグランドに接地されているので、バーチャルグランドで 反転入力端子もグランド電位(0V)に固定されることになります。
その結果、R1~R4のすべての抵抗の片端は0Vに固定されます。すると、各抵抗に流れる電流と抵抗値を掛けると 反対端の電圧になるわけです。つまりV1、V2、V3、Voutの4つの電圧はオームの法則により各抵抗×電流の掛け算式 で表されます。
例によって、オペアンプの入力インピーダンスは無限大なので、反転入力端子に流れ込む電流はゼロです。よって、 R4に流れる電流i4はi1+i2+i3、つまり入力電流のすべての合計になります。
以上を加味して式から電流を消去して整理すると、Vout=(V1/R1+V2/R2+V3/R3)×R4となります。 帰還抵抗R4が全体にかかる増幅率の決め手となります。反転増幅回路の帰還抵抗と一緒で、大きい抵抗値にすれば 出力電圧が大きくなります。
ちなみに、もしR1、R2、R3、R4に等しい抵抗値を適用すると、Vout=V1+V2+V3となり、出力電圧が 各入力電圧の合計になることが判ります。
先述のとおり、入力電圧の合計値と出力電圧の符号は逆転していますのでご留意ください。
ちなみにR1、R2、R3、R4に別々の値を設定すれば、単純な足し算だけでなく加重を付けて合算することも出来ます。 計算式をご覧頂くとお分かりのように、個々の増幅率はそれぞれR4/R1、R4/R2、R4/R3になります。
このように、加算回路でも「バーチャルショート(バーチャルグランド)」「入力インピーダンスが無限大」「オームの法則」 を応用することで簡単に計算式が導き出せることがおわかりいただけると思います。
使用上の注意
基本的には足し算の為に使われる回路なのであまり増幅率を大きくして使うことは少ないと思いますが、 帰還抵抗R4を大きく取って増幅率を何百倍・何千倍にも増幅するのには向きません。その辺は反転増幅回路と同様です。
例
単純な足し算をする回路を考えてみましょう。R1~R4に10kΩを適用してみます。R1=R2=R3=R4なので 計算式から抵抗値が消え、出力電圧VoutはV1+V2+V3と簡単な式になります。
クリックするとページの上部に戻ります。減算回路(差動増幅回路)
特徴
2つの入力電圧の差分を求める回路です。(例えば5V-2V=3Vといった具合です)
減算回路は、これまでに挙げた非反転増幅や反転増幅等と比べると、少し複雑な動作をしています。
これまでは、反転入力や非反転入力のどちらかが(直接もしくは抵抗を介して)グランドに接地されていて、 その部分が”てこ”でいう支点になっていましたが、減算回路の場合はちょっと違います。
減算回路の支点は反転入力端子です。ただしこの反転入力端子はバーチャルショートで非反転入力端子と同電位。 一方、非反転入力端子は入力電圧を抵抗で分圧した値なので、入力電圧の変動によって上下します。つまり支点自体が 入力信号によって上下に変動するわけです。
でも、基本はこれまでと一緒。「バーチャルショート」「入力インピーダンスが無限大」「オームの法則」の3つを応用 すれば計算式は簡単に理解できてしまいます。
回路図と計算式
入力電圧V1からV2を引いた電圧を出力する回路について考えて見ます。

まずは非反転入力端子の電圧について着目してみます。この端子に掛かる電圧V3は、入力電圧V2を抵抗R2とR4で分圧した値となります。 これが図中の一番上の式です。
すると、バーチャルショートで反転入力端子も同電圧(=V3)となります。このことを元にして、R1とR3の2つの抵抗の各両端に 掛かる電圧について考えることが出来るようになります。
R1に流れる電流をi1と置くと、オームの法則からR1に掛かる電圧はR1*i1。同様にR3に流れる電流も R3*i1となります。(オペアンプの入力インピーダンスは無限大なのでR1とR3に流れる電流は等しい)
するとV1とV3の関係は V1+R1*i1=V3となり、V3とVoutの関係はV3+R3*i1=Voutという、
2つの式が導き出されます。
(ちなみに、両端の電圧の差に着目し、それぞれV3-V1=R1*i1、VOUT-V3=R3*i1という式にしても
同じ結果が得られます。お好きな方でどうぞ)
これらの式からV3とi1を消去していくと、Vout、V1、V2の関係を抵抗値で表す式に変形できます。ちょっと複雑ですが…
このままだと複雑でちょっと使いにくいので、例えばR1~R4の4つの抵抗をすべて同じ値だと仮定してしまいます。すると計算式は、 Vout=V1-V2と、極めてシンプルな形に変形できます。つまりV1からV2を引いた電圧が出力されるというわけです。
もう少し応用範囲を広げるために、引き算した電圧値に定数倍の増幅をかけることを考えてみます。R1=R2、R3=R4と 設定し、先ほどの複雑な式に入れてみてください。すると、Vout=(R3/R1)(V2-V1)という式が 現れます。これは、V1とV2の差分にR3/R1倍の増幅をかけた電圧が出力されることを意味しています。
計算途中はちょっと複雑な感じですが、式を整理するととてもシンプルな形に整理できることがわかります。
使用上の注意
アナログ回路を設計する上で、注意が必要な事柄の1つは「差を取ると相対的に誤差が拡大する」ということです。
減算回路は、当然ながら「差」をとる回路ですので、この注意点に抵触します。さて、その「相対的に誤差が拡大する」とは どういうことでしょうか?
例えばV2=5V、V1=3Vであると仮定します。理論上では、(V2-V1)=2Vとなりますね。 ところが、アナログの電圧とは大なり小なり誤差を含んでいるので、実際に入力される電圧は5Vとか3Vとかに多少の誤差が含まれています。
では、その誤差を含めて計算をやり直して見ましょう。
例えばV2の電圧に5%の誤差を含み、5.25Vになっていたとします。すると、その差を計算すると 5.25V-3V=2.25Vです。本来2Vにならないといけないのですが出力結果は2.25Vですから、その誤差の割合は (2.25V-2V)÷2V×100%=12.5%!!! 5%から12.5%へ誤差が大幅に増えてます!
相対的に誤差が増えるというのはこういう意味です。なので差分を取るアナログ回路の場合、入力電圧を出来るだけ正確にしておく とともに、各抵抗(図のR1~R4)には金属皮膜抵抗など誤差が小さいものを使う必要があります。
もう一点。
図をパッと見てお気づきのように、入力側にいっぱい抵抗が繋がっています。こういう場合、オペアンプ自体には電流の流出入がなくても、 抵抗を通し、入力側からグランドや入力側から出力側に若干電流が流れてしまいます。その時に、入力側に繋がっている回路に対して 影響を及ぼすことがあります。(抵抗を含めると入力インピーダンスが低くなってしまう)
入力インピーダンスを高めるためには、この回路の代わりに「インスツルメンテーションアンプ回路」を使ったり、 または入力側に1段オペアンプをかまして入力側の電圧を固定させるなどの手当てが場合によって必要となります。
なお、絵ときでわかる オペアンプ回路に載っている回路によると R4は使われていません。R3、R4による抵抗の分圧ではなく、入力電圧V2をR3を介して直接非反転入力端子に供給しています。 (その場合のR3は両入力端子のインピーダンス整合用のようです。R3を省くとオフセットが生じてしまうために R3を残してあると思われます。インピーダンス整合については別途触れます。)
R3、R4の抵抗分圧を使ったほうが応用が利きそうだなぁというのと、加減算回路を理解する際にこの回路の 考え方が理解できている方が良さそうだと思ったので、今回は上図のような回路で説明しました。
例
V2からV1を引き算してそれを2倍にするという回路を考えてみます。計算式でいえば、Vout=2*(V1-V2)です。
例によって、1kΩ~100kΩに収まる程度で考えます。R1=R2=10kΩ、R3=R4=20kΩに設定すると、 Vout=R3/R1*(V2-V1)=2*(V2-V1)となります。
クリックするとページの上部に戻ります。加減算回路
特徴
正値、負値それぞれ1個以上の電圧を入力し、それらすべてを加減算した電圧を出力する回路です。
2つのオペアンプを使っていますが、両方とも加算回路として働いています。加算回路は先述のとおり、 複数の入力電圧を合算してそれを反転(負値)して出力する回路です。
よってこれらの回路を2回通過すればマイナス×マイナスでプラスの値に、1回だけ通過すればマイナスの値として 合算され、それらの合計が出力端子に現れるというわけです。
回路図と計算式
2つの電圧を正値、2つの電圧を負値として計4つの電圧を入力し、それらを加減算して出力する回路を考えてみることにします。
パッと見は複雑な回路のようですが、何のことはありません。加算回路を2つ直列に繋いだだけですから!前段、後段の各 オペアンプについて、それぞれが加算回路を成していることを、図を見てご確認ください。
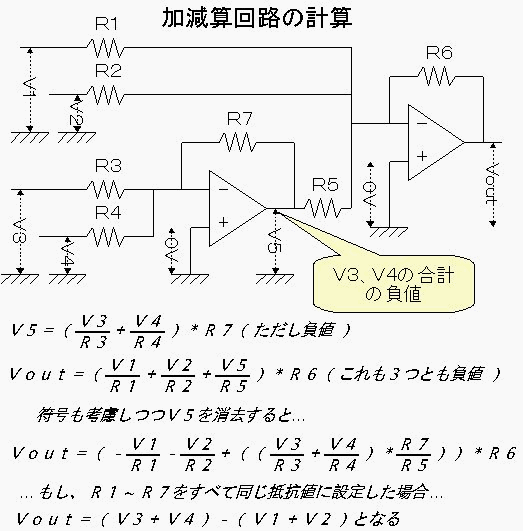
まず、前段のオペアンプについて考えてみます。入力電圧はV3、V4、出力電圧はV5となっています。前段は一つの独立した 加算回路なので、入力電圧V3、V4を合算して負値として出力する働きをもっています。よって、V5部分の電圧は図中のような式で 表されます。
後段のオペアンプも加算回路として働いています。すると後段は、V1、V2、V5の3つの電圧を入力とする3入力の加算回路と 考えることが出来ます。出力電圧Voutは図の計算式のとおりV1、V2、V5の3つの電圧と抵抗値で表すことが出来ます。
V1、V2は加算回路を1回、V3、V4は加算回路を2回、それぞれ通過することになるので、V3、V4はプラスの値でV1、V2は マイナスの値で出力されることがおわかりいただけると思います。
計算式からV5を消去すると、VoutはV1、V2、V3、V4と各抵抗値で表すことが出来ます。
このままではちょっと複雑なので、R1~R7の各抵抗値を同じ値と仮定すると、すべての抵抗が式から消去でき、 結果、Vout=(V3+V4)-(V1+V2)という、とってもシンプルな計算式が現れます。
使用上の注意
今回は正値2入力、負値2入力の計4入力を例に取りましたが、各々1個以上の入力電圧を繋げば加減算してくれます。 なにしろ、加算回路(反転加減算回路)を2段直列につないでいるだけなので…
また、R1~R7をすべて同じ値にした場合を例に取りましたが、これらのうちR6、R7は加算回路でいうところの増幅率を 決定する抵抗にあたります。なのでこれらの値を適当に調整すれば出力電圧に適度な加重をかけることが出来ます。 必要に応じて計算式を変形してみてください。
ちなみに、加減算回路も”減算回路”の機能を含んでいるので、「差を取ると相対的に誤差が拡大する」ということに 注意が必要です。詳しくは減算回路の部分をご覧ください。
例
例を挙げるまでも無いですが、R1~R7をすべて10kΩに設定するとします。
すると、Vout=(V3+V4)-(V1+V2)と、シンプルな出力結果が得られます。
クリックするとページの上部に戻ります。もう一つの加減算回路
特徴
働きとしては、上記の加減算回路と基本的に同じものです。
加減算の演算を行うためにオペアンプを2つも使うのが嫌だなぁ、オペアンプって反転/非反転2つの入力があるんだから、 上手くやればオペアンプ1個でも加減算できるんじゃないかなぁ、っていういつものケチケチ根性でネットの海をさまよっていたら、 ↓こういうのを発見しました。
大阪大学基礎工学部機械工学科の「オペアンプを用いたアナログ回路」 加減算器の記事
こちらのサイトで公開されている回路は、オペアンプ1個で正値2入力負値2入力の加減算回路を実現しています。上述よりも オペアンプが1個少なく構成されてます。計算式は恐ろしく複雑になりますけどね…
考え方さえ解ってしまえば、入力信号の数は好きなように増減できるはずなので、このページでは上記の参考サイトとは 違う構成の回路について考えてみたいと思います。でもやっぱり、「オームの法則」「バーチャルショート」「入力インピーダンス=無限大」 の3つを応用すれば計算が出来るのは一緒です。
回路図と計算式
この回路の計算式をそのまま再計算してみてもあまり面白くないし、Chanさんのサイトの コンポーネント-RGBコンバーター のページの一番下、参考回路4(逆変換) に出てくる回路の考え方を解読したり、ビデオ関係の信号生成回路を自由に設計するための考え方を整理しておきたいという 当面の目標があるので、Chanさんの回路中に現れる2種類の加減算回路「正値1入力、負値2入力」「正値3入力、負値1入力」 の各加減算回路について図解してみたいと思います。
- まずは正値1入力、負値2入力です -
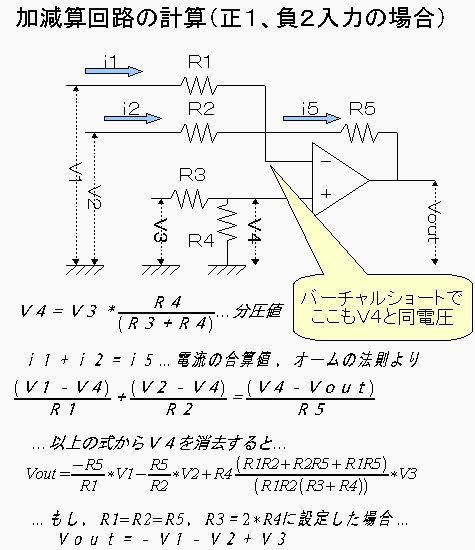
まず非反転入力側に掛かる電圧について着目します。
入力端子のインピーダンスは無限大なので、入力電圧V3をR3、R4で分圧した電圧V4が非反転入力に かかることになります。するとバーチャルショートで反転入力端子もV4となることが判ります
次に非反転入力端子に関わる抵抗R1、R2、R5に流れる電流i1、i2、i5について着目します。
例によって入力端子のインピーダンスは無限大なので、i1とi2の合計の電流がi5となることが判ります。 これらの電流は、オームの法則により各抵抗値と抵抗に掛かる電圧値で求めることが出来るので、 式からi1、i2、i5を消去することができます。
さらに、2つの式からV4を消去して整理すると、VoutはV1、V2、V3と抵抗値で表される式になります。
このままではちょっと複雑なので、もう少し簡単な式に変形することを考えてみます。R1=R2=R5、およびR3=2*R4 と仮定してみると、この式はVout=-V1-V2+V3というシンプルな式に変形することが出来ます。
- 続いて正値3入力、負値1入力です -
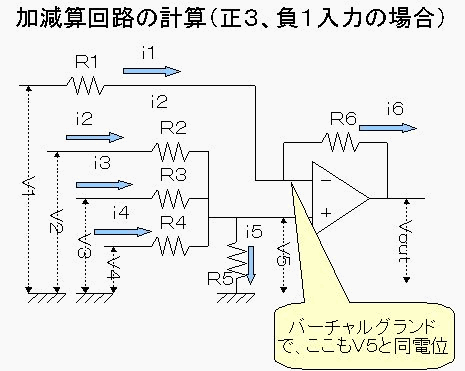

反転入力端子・非反転入力端子に掛かる電圧=V5と仮定してみます。(バーチャルショートで同電圧です)
まず非反転入力側の各抵抗R1、R6にかかる電流に着目してみると、入力端子のインピーダンスは無限大なので、 i1=i6となります。これをオームの法則とV5の電圧を用いて電流を消去すると、図中のような式に変形できます。
次に反転入力端子に関わる抵抗R2、R3、R4、及びR5に流れる電流について考えます。入力端子のインピーダンスは 無限大なので、i2+i3+i4=i5となることが判ります。
この式からも同様にオームの法則を用いて電流を消去すると、図中のような式に変形できます。
これらの2つの式からV5を消去して整理すると、VoutはV1、V2、V3、V4及び抵抗値で表される式になります。 実はこの計算の過程が物凄く長くて大変なのですが…省略します。お暇な方は一度チャレンジを!
図中のαは、式を見やすくするために式中の共通項を括りだしたものです。深い意味があるわけではありません。
いずれにしてもこのままでは複雑過ぎるので、もう少し簡単な式に変形することを考えてみます。R1=R6、および R2=R3=R4=3×R5と置いてみると、Vout=-V1+V2+V3+V4とシンプルな式に整理できます。
なお、Chanさんの回路図では、負値入力側端子の働き方がかなり特殊です。
負値入力側にはデジタルトランジスタを用いることで5VかHIGH-Zのどちらかが掛かるという特殊な動作になっています。 特にHIGH-Z入力状態での動作は、正値側の3つの入力電圧を抵抗比で合成しながらボルテージフォロアで出力するというような 動きになっています。その点が純粋な加減算回路とちょっと違っています。私の想像ですが、このような複雑な抵抗計算を避ける 目的だと思われます。(詳しいことは後ほど纏めます)
今回このページでは、純粋に加減算回路として働いた場合にどの様な動きになるかをきちんと整理しておきたかったので、 あえて難解な計算式に挑戦してみました。入出力の数がこれと同じならそのまま適用できるので、必要に応じて ご使用ください。
使用上の注意
先述のオペアンプを2個使う加減算回路と比較して、オペアンプ1個で組める便利な回路です。今回は上記の2つを 例にとってみましたが、入力端子が幾つあっても計算の考え方は一緒(のはず)です。
ただし、オペアンプを2個使うタイプと違って抵抗値の計算がヒジョーに複雑で厄介です。しかも入出力端子が増えたり減ったり するたびに複雑な計算式をその都度書き出さないといけません。(オペアンプ2個の場合なら、入出力が幾つでも全抵抗値を同じに することで簡単に足し算引き算が出来ることとは対照的ですね)
複雑な抵抗計算をゴリゴリ行ってでもオペアンプの数を減らすか、それともオペアンプを2段に構えて計算の手間を省くかは、 作業労度やコストなどを念頭にご判断いただければと思います。
これらは基本的に加減算が目的となる回路だと思うので、比較的小さい増幅率で使われることが多いでしょうから 抵抗値計算時にインピーダンス整合を考慮する必要はないかと思います。もし増幅率を大きく取るような抵抗値を選択する場合は、 オフセットが狂わないように両入力端子のインピーダンス整合をきちんと考える必要があるかと思います。 (インピーダンス整合については後々触れます)
ちなみに、加減算回路も”減算回路”の機能を含んでいるので、「差を取ると相対的に誤差が拡大する」ということに 注意が必要です。詳しくは減算回路の部分をご覧ください。
今回挙げたどちらの例においても、適当な抵抗値を選択することで、オペアンプ1個でも加減算回路が組めることが 判るかと思います。今回は、ビデオ信号用演算回路に応用できるような入力端子で考えましたが、これは後々に向けた伏線です。 必要に応じて、入力端子を増減した回路を組んで、計算してみてください。
例
例1:正値1入力、負値2入力の場合
R1~R5を1kΩ~100kΩに収めるとして考えます。R1、R2、R3、R5を20kΩ、R4を10kΩと おくと、Vout=-V1-V2+V3となります。本当は反転入力端子・非反転入力端子双方に繋がるインピーダンスを 整合させないとオフセットが生じるはずなんですが、ひとまず考慮しないことにします。
例2:正値3入力、負値1入力の場合
同様にR1~R6を1kΩ~100kΩに収めるとして考えます。R1、R2、R3、R4、R6を30kΩ、R5を 10kΩとおくと、Vout=-V1+V2+V3+V4となります。同様に入力端子に繋ぐインピーダンスの整合を 考慮しないといけないのですが、割愛します。
クリックするとページの上部に戻ります。インピーダンス整合
インピーダンスとは
インピーダンスとは、交流回路における電気抵抗成分のことで、「レジスタンス=直流と交流の両方にはたらく抵抗成分」と、
「リアクタンス=交流だけに働く抵抗成分」を足し合わせたものです。
リアクタンスには、「インダクタンス」成分と「キャパシタンス」成分があり、インダクタンスは「コイル」などのように、
電流の変化を妨げる方向で働き、キャパシタンスは「コンデンサ」のように電荷をためる働きを持っています。
交流の電圧を「抵抗」に掛けた場合、電流はその電圧の「位相」と同じように上下します。
コイルやコンデンサなど「インダクタンス」を持つパーツに交流を掛けた場合も、電流は上下します。 しかし、コイルのように「インダクタンス」を持つ「インダクタ」の場合は「位相」が90度遅れて電流が流れ、 コンデンサなど「キャパシタンス」を持つ「キャパシタ」の場合は「位相」が90度進んで電流が流れます。 (「抵抗」「インダクタ」「キャパシタ」を組み合わせた場合は、 位相が「90度」単位ではなく中間的な位相にずれた電流が流れます)
また、同じインダクタンス、キャパシタンスに対していろいろな周波数の電圧を掛けると、
周波数によってそのインピーダンスは変化します。周波数が高くなると、インダクタンスのインピーダンスは高くなり、
キャパシタンスのインピーダンスは低くなります。
(つまり、インダクタンスは高い周波数を通しにくく、キャパシタンスは高い周波数を通しやすい)
さらには、「コイル」や「コンデンサ」に限らず、「ただの導線」や「基板上の配線」も、若干の「インピーダンス
(リアクタンス)を持っています。そのため、特に高周波を扱う回路では、「ただの配線」が大きなインピーダンス
(リアクタンス)となり、悪影響を及ぼすことがあります。
また、コンデンサは純粋な「キャパシタンス」成分だけではなく、同様にコイルも純粋な「インダクタンス」成分だけではありません。
それぞれ「レジスタンス」「キャパシタンス」「インダクタンス」を併せ持った電子部品となっています。
インピーダンス整合とは
回路中の「信号の発生源」から「信号の伝達先」まで信号を伝える際、インピーダンスの影響を含めると、 その経路の配線(プリント基板上の配線や、機器同士を繋ぐケーブルなど)が、「インダクタ」や「キャパシタ」 としてもはたらくようになるため、交流成分の信号が鈍って振幅が小さくなったり、 配線内で信号が反射して往復してしまってオーバーシュートやリンギングが発生したりします。
そのような影響を受けないように、「信号の発生源」から「信号の伝達先」まで意図した信号を送るためには、 送り出す側と受ける側の「インピーダンスの値を同じ(※)にする」ことが必要になります。 それをインピーダンスマッチングといいます。
(※:後述しますが、「同じ」というよりは、出力側と入力側のインピーダンスが、お互いに「複素共役」 の関係になっている状態が「整合」した状態)
「Z1=Z2=Z3」の時に、インピーダンスが整合していて、負荷で消費するエネルギーが出力になります。(最大効率)
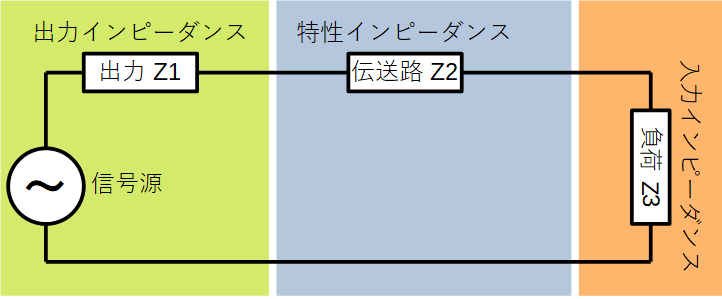
参考サイト
https://www.jp.tdk.com/techmag/inductive/201110/index2.htm http://www.iccraft.com/parts/s_imp.html
インピーダンス整合していないと…
インピーダンス整合していないと、信号が反射したりノイズが起きて、意図しない信号が伝わったり、 信号源からのエネルギーが負荷に効率的に伝わらないといったことが起きます。
回路図上では、単にICの出力端子を別のICの入力端子に接続していると描かれているだけの回路でも、
実際の基板上の配線では、「回路図にないインピーダンス」が存在しており、これが悪影響を及ぼすことがあります。
つまり、ただの導線や基板上の配線にも寄生インダクタ/キャパシタの成分が存在しており、高周波の場合に顕著に影響を及ぼします。
(また、配線が長ければ、その経路中に寄生しているインダクタンスやキャパシタンスが大きくなりますが、
必ずしも短ければ大丈夫というわけでもなく、配線の長さによって固有の共振周波数をもつので、短くしたら逆にノイズが増える、
ということもあり得ます)
インピーダンス整合が現れる例
例として、どのような時にインピーダンス整合が考慮された回路になっているかを探してみましょう。
例えば、「ビデオ信号ケーブルと入出力回路」が挙げられます。ビデオデッキなどの機器から出力されるビデオ信号は、 先ほどの図では、各インピーダンスが
「Z1 = Z2 = Z3 = 75Ω」
となっていると、エネルギー効率100%で、反射によるノイズも少ない状態で、ビデオ信号を伝えることができます。
最近は殆ど使われることがなくなってしまった「SCSI」というPC周辺機との接続規格がかつてありました。 この「SCSIケーブル」には50Ωの「終端抵抗」を取り付けることで、反射波を発生させないようになっています。
また、オシロスコープの「プローブ」は、そのままではプローブ自体が持っている「インダクタンス」「キャパシタンス」によって、 信号波形が変形してしまうため、波形が鈍ったりオーバーシュートしたりしないように、位相を調整するトリマが付いていいます。
インピーダンスマッチング回路
私はあまり交流回路や交流信号は得意でないので、「こうしたらバッチリ!」とか「こういう風に回路を設計しよう!」 といったことを明確に説明できませんが、色々と調べてみた範囲で、「どんな風にすればいいの?」「どんなこと考えるの?」 といったことを、理解の範囲でメモにしておきたいと思います。
まず、デジタル信号や、オーディオ信号、ビデオ信号といった信号を扱う際について考えてみます。
例えばビデオ機器では、ビデオ信号用ICの出力端子から出力した信号を、外部のケーブル配線を通して伝達し、 入力機器側で入力するという、一般的な配線を考えてみます。
入力側回路側では75Ωで受けるようになっており、これに合わせて出力IC側の出力回路も75Ω抵抗を通して出力するようになっています。 これにより、伝送経路中で反射波が発生したりしないようになっています。(加えて、75Ωケーブルを使用)
上記の「SCSI」の終端抵抗も、同じような考え方で「50Ω」で出して「50Ω」の抵抗で受けることで、信号の反射を抑えたりしています。
これらの入力側、出力側に付ける50Ωや75Ωの抵抗について、まだちゃんと理解できたところまで至ったとは思えていないのですが、 Z1、Z2、Z3が等しい状態とはどんなことなのかについて調べてみると、「インピーダンスが整合」している状態とは、 特に入力側(Z1)と出力側(Z3)のインピーダンスがお互いに「複素共役」になっている状態であると良いみたいです。
インピーダンスは、実数成分である「抵抗成分(レジスタンス)」と、虚数成分である「インダクタンス+キャパシタンス(=リアクタンス)」
を足したものなので、「複素数」として表現できるわけです。
「複素共役」とは、この「虚数成分」の正負を逆転したものです。
出力側のインピーダンスが実質抵抗成分だけ(実数だけ)で、入力側のインピーダンスも実質抵抗成分だけ(実数だけ)であれば、 「虚数成分=0」なので、同じ抵抗値の抵抗を使うことで、当然複素共役の関係になっています。
(調べてみてまだよく解らなかったのは、伝送経路中のZ2のリアクタンスやキャパシタンスはどうなるの?といった点)
なお、扱う信号の周波数帯によって、インピーダンス(特にリアクタンス)が変化してしまいます。 そのため、抵抗だけではなく、回路の構成や扱う信号の周波数によっては「LC回路」を挿入して整合を図る場合もあるようです。
実際の回路を組む際にどう考えるか
交流回路の計算については、以前「交流の回路計算」という本を読んで、 その当時はLCR回路の計算なんかを「なんとなく」理解していたんですが、Arduinoとかmbedとかでデジタル信号ばかり扱っていると、 あまりこのあたりを気にしなくても回路が動いてしまうので、すっかり忘れてしまっています。 あらためてもう一度読み返してみたいなと思うところ…。
というわけで、周波数帯によってインピーダンスは変化するので、どんな回路であっても万能な「最適解は存在しない」ようです。 そのため、誤差やノイズを小さくするものを探し出して選択することになるようです。(次善解)
比較的低周波である「音声信号帯~数MHz」程度の場合は、基板上の配線や基板間のケーブルにおけるリアクタンスはそれほど大きくはありません。なので、小型のプリント基板内での信号伝達なら、あまり気にしなくても動作すると思います。しかし、10MHzを超えてくるあたりから、 影響が大きくなっていくようです。
ただし、数MHz以下でも、伝送経路の配線が長くなる場合(機器同士をケーブルで繋ぐ)などは、考慮する必要があるでしょう。
さらに高周波となる、最近のPC内部の通信回路(メモリの入出力や内部バスによる通信のように、数百MHz~数GHzといった領域)や、
さらには無線などで利用するRF帯の場合は、このあたりの影響は低周波とは影響度合いが異なるので、きちんとした設計が必要になるでしょう。
「これだけ知ってれば、大丈夫、これだけ守ってれば大丈夫」というものはないので、自作や設計難しそうです。
特にRF帯領域では、どんなふうにしているのかなと思って、RF帯の信号を分波したりする「RFパワーディバイダ」回路を検索してみました。
RFコンポーネンツ などでは、専用パーツを扱っていたりするみたいです。やはりこういった高周波数帯では、 専用パーツを使うのが一般的みたいです。
このページのまとめ
このページでは、主に加減乗除に関わる回路について触れてきました。表中にあるようにこれら以外にも沢山の 回路がありますが、それらは今後必要に応じて触れていきたいと思います。
このページで挙げた回路は、入力と出力が一次式であらわされる回路(線形回路)ばかりですが、 この範囲内であれば、「オームの法則」「バーチャルショート」「入力インピーダンス=無限大」の3点の応用だけで 様々な回路に応用できることがお判りいただけたと思います。
これらの考え方を元にして、次のページでは 実際の作例についてその働きを解読していきたいと思います。(クリックして進んでください)





