PIC AVR 工作室->TopPage->資料倉庫->FFT・複素数入門2
FFTの計算と複素数の入門2
波、回転と「三角関数」「複素数」
改めて三角関数
波とか回転といった現象(物理現象)を扱う時、真っ先に登場するのは三角関数でしょう。
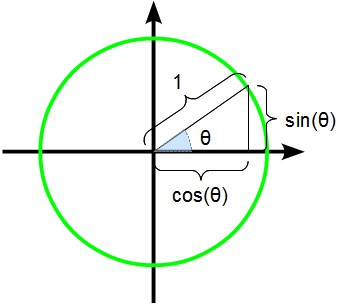
三角関数は、図の様に半径が1の単位円があって、その中心からその円周の点に向かった線がx座標と角度=θをなしているときに、 x座標の値がcos(θ)、y座標の値がsin(θ)となると習いました。この角度θとcos(θ)とsin(θ)をグラフにするとこのように波型になります。
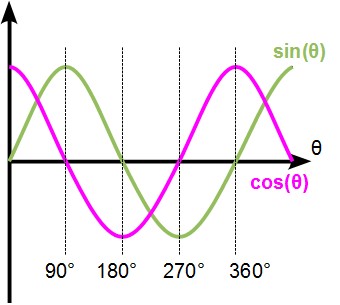
このように、波とか回転とかいう場合には三角関数はきっても切れない関係があるわけです。
この三角関数を使うと、下の図の様に「ある座標の点」に対して任意の角度で移動(変換とか回転とか言う計算処理)することができます。 この例であれば、座標(x,y)からθ度回転した(x',y')の座標を計算することができます。
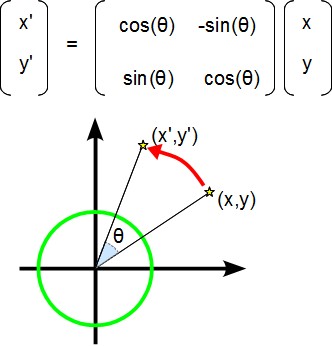
DFT計算についても、この「回転」を使う計算が現れます。現れるというより、この回転計算を大量に行う必要があります。
回転計算とDFTのイメージ
先ほどの図に少し書き足したものです。
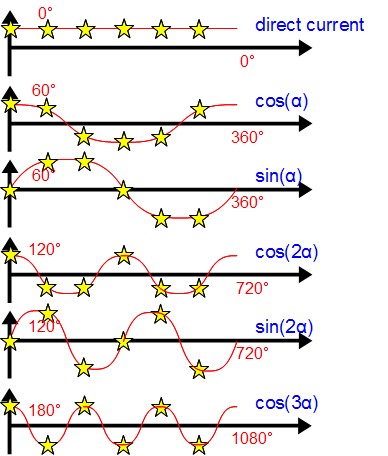
この図の横軸は時間経過に比例する「位相」で、星印のy座標はそれぞれサンプリング値と比較するための単位ベクトルの「成分」をあらわしています。 一番上の波形(直流成分)なら、時間の経過に関わらずy軸は同じ値をとり続けるので、全成分が「1」になっています。 その1つ下の波形(cos成分)なら、時間の経過に伴ってcos(余弦)波のようにy軸が上下しています。星6個でcosの1波形分です。 さらにその1つ下の波形(sin成分)も同様に星6個で1波形分です。さらに下に行くと曲線の周波数は2倍、3倍…と細かくなっていきます。
これらの「波」と、サンプリングしたADCデータとの内積を取って類似性を一つ一つ計算すれば、各周波数毎の成分が抽出できることになります。
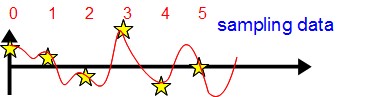
6点DFTなら、サンプリングした6個のデータと、これらの横6個分のデータの組(単位ベクトルの1組分)との間で内積をとれば、 その内積の値が該当周波数における成分の量ということになります。このようにサンプルデータと各波形の内積を求めていけば、 直流から最高周波数までの各周波数の成分に分離(つまりDFT計算)できることになります。
(ちなみに内積値がマイナスの場合はベクトルが反対向き、つまり位相が180度ずれていることを表します)。
さて、この直流~三倍周波数のcosまでの星印のy座標はどうやって求めるのかというと… 直流は考えるまでもないでしょうが、常に一定の値ですね。具体的にはy座標をすべて「1」としておけばokです。
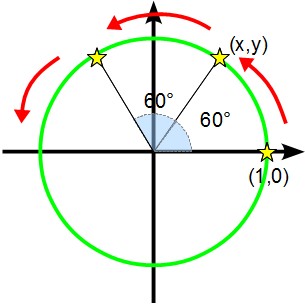
2列目(cos波形)は、ひとまずこんな風に考えてみます…一番左の星印は半径=1の単位円上の座標(1,0)にあって、 そこから順に(360度÷6点=60度)ずつ点が単位円上を移動(回転)していき、そのx座標を順に取り出すとさっきの波形のy座標がもとまる、と。
このように掛け算を繰り返しすることによって、一定角度分ずつの回転を表現できます。
さらに1つ下の波形(sin波)ならy座標を取り出して波形のy座標とします。その下の2倍周波数のcosなら720度÷6=120度ずつ回転していけばokです。 720度というのは(360度×2倍)の値、つまりcos波が2つ分の角度。
一見ややこしいように見えるかもしれませんが、このように星印が一定角ずつ回転していくという考え方を使うと、 その「回転角」を変数とすれば直流~最高周波数まですべてを同じ計算方法が適用できて便利なのです。 (なお、一般的なDFT/FFTの計算では回転方向はこの図と逆になっていると思います)
さっきの図の曲線、上から順に「直流成分」「1倍周期cos」「1倍周期sin」「2倍周期cos」「2倍周期sin」「3倍周期cos」は、 それぞれ1回あたり0度、60度、60度、120度、120度、180度の角速度で回転させてやれば各星印のy座標が順々に求まります。 そして各6個を束にしたベクトルとサンプリングした6個のデータ(ベクトル)のそれぞれで内積を求めていけば、DFT計算ができることになります。
これらの各周波数のベクトルとサンプリングデータの内積を取るということは、 つまり各周波数毎のベクトルとの類似性を数値化(スカラー化)しているわけです。
このような、各周波数に相当する単位ベクトル(直流、1倍cos波、1倍sin波、2倍cos波…)の各6個の要素それぞれを組にして、 回転因子(twiddle factor)などといいます。6点DFTならこんな感じ。
(cos(0),cos(0),cos(0),cos(0),cos(0),cos(0)) …直流 (cos(0),cos(60),cos(120),cos(180),cos(240),cos(300)) …1倍cos波 (sin(0),sin(60),sin(120),sin(180),sin(240),sin(300)) …1倍sin波 (cos(0),cos(120),cos(240),cos(360),cos(480),cos(600)) …2倍cos波 (sin(0),sin(120),sin(240),sin(360),sin(480),sin(600)) …2倍sin波 (cos(0),cos(180),cos(360),cos(540),cos(720),cos(900)) …3倍cos波
このように、6×6個の要素で構成される回転因子ができます。
たぶん正確には後述するように複素数のべき乗表記したものを回転因子と呼び、 このようなごちゃごちゃsin/cosで書いた行列は単に「変換行列」などと呼ぶんだと思いますが、 とにかく「2π/n」ずつグルグル回転していく点を表す要素で構成した行列なんだなぁということです。 …なお行列とベクトルの概念をイイカゲンに書いているのでその点はご注意ください。
この例では6サンプルでしたが、サンプル数が6個ではなく100個や1000個と増えた場合でも星の数が増えるだけなので、考え方自体は一緒。 星それぞれの角速度に応じて回転計算を行い、ベクトルの内積を順々に求めればDFTの計算ができるわけです。
ちなみに、同じ周波数でcosとsinのペアがあるのですが、これは各周波数における「位相」を表現する為のものです。 cosが0度、sinが90度と置くと、例えばサンプリングしたデータ中の該当周波数の位相が45度の場合はcosとsinに半々に分かれて現れます。 位相が180度なら「-cos」として現れるといった具合です。
DFTのリクツはだいたいそんな感じです。実際、このような原理で三角関数を用いてDFTを計算することは可能です。
(注:このままだと、各ベクトルの長さが1にならないので、ベクトルの長さを1にそろえる「正規化」という作業が必要…後述)
これまでのことを利用してDFTの計算をしてもいいかもしれませんが、2つ面倒なことがあります。 一つは三角関数を用いて回転計算をするのがいちいち面倒なのと、もう一つはサンプル数が増えると指数関数的に計算量が増えて、 実用的には役に立たないほどの処理時間を要することになることです。(回転因子はサンプリング数の自乗の個数があることに留意)
前者に対しては複素数による計算で、後者に対してはDFT→FFTの計算へと基軸を切り替えます。
回転計算と複素数について
複素数についてザックリ触れてみます。
虚数単位というのがあります。数学では小文字の「i」で表して、このiを2回掛け合わせると「-1」になるという数字のことです。 電気の世界では、電流「i」と区別する為に小文字の「j」を使います。このjを使って複素数はa + jbの形で表します。 (a + bj とは一般には書きません…注意)
で、いきなりですが複素数では掛け算は「回転」を表します。そんなこと習ったことすら忘れていた私には、 本を読んだときにはいきなりで面食らったのですが、グラフで書いてみると実際そうなります。試しに、「1」に「j」を掛けていってみましょう。
1にjを掛けるとjです。jにjを掛けると-1です。-1にjを掛けると-jです。-jにjを掛けると1に戻ります。プロットしてみます。
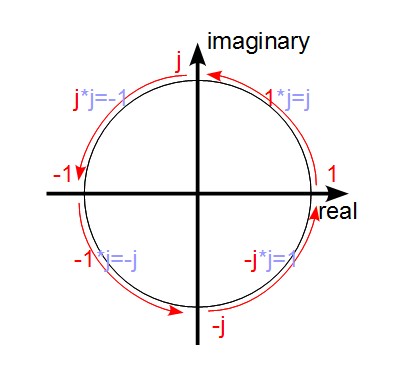
こんな風に、虚数「j」を掛けると90度の回転が表現できます。実はjだけじゃなくて、複素数全般を掛ける場合も同じように「回転」を表します。
jを掛ける以外の計算も一応見てみましょう。例えば(1+2j)と(-2+0.5j)を掛けてみます。すると(-3-3.5j)となるはずです。プロットすると…
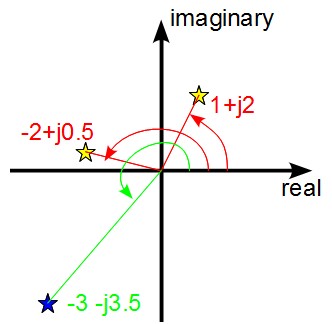
こうなります (三平方の定理と三角関数を使えば実際にこの図のように回転が表現できていることが計算できるんですがこのページでは計算過程は省略します)。
まぁ、この図のように掛け算を行うと、 (1+2j)が表す角度に(-2+0.5j)が表す角度の分だけ回転したところにその解の(-3-3.5j)があるということを掴んでください。 (この図の2つの赤い角度を足すと緑の角度になる…つまり掛け算は「回転」)
この図の場合、掛けた数(-2+0.5j)の「長さ」が「1」よりも長かったので、掛けた結果は「回転」だけでなく「長さ」にも影響してしまいました。 長さが1となる複素数(実数部と虚数部それぞれの2乗して足して平方根を取った値が「1」となる)を掛けた場合は、 長さは元の複素数と同じままで、角度の分だけ回転した結果が得られます。
jとか-jは長さが「1」の複素数の代表例なので、これを掛けると長さはそのままで90度回転します。 なお、この長さが1の複素数っていうのがさっき出てきた「正規化」と絡む話になります。正規化については後ほどまた改めて。
複素数のべき乗計算
掛け算で回転を表すことが出来ました。さて、さっきも触れたようにDFT計算では一定角の回転計算を大量に行います。 先ほどの例では60度ずつ連続して回転するという図が出てきました。このような回転計算が大量にでてきまます。 例えば60度を2回、3回、4回、5回…と連続して掛け算する(回転する)計算を行うことになります。
三角関数は計算に時間が掛かるので回転の計算を行うのは結構大変ですが、複素数を使って連続回転をさせる場合は簡単になります。 複素数による回転計算は、三角関数を持ち出すのではなく、複素数の「べき乗」計算をすればokです。 たとえば、n=0,1,2,3,4,5,6…の時にjのn乗の計算を延々とおこなえば、nが1増えるたびに90度ずつ順々に回転していくことを表すことができます。
DFT計算ではsin/cosによる行列計算の代わりに、複素数の掛け算(というかべき乗)を用いることで省力化できます。
昔、学校で複素数のことを習った当時、「想像上の数なんて習って、一体何の役に立つんだよ!」と思ったものですが、 こういう風に「回転の計算を楽に行うツール」と割り切ってしまえば、これはこれで超便利な道具というわけです。
複素数に限った話ではないですが、ベクトルや行列のような「代数幾何」で習う物は所詮「計算を楽に済ますツール」であって、 表記方法になんぞこだわらず、「道具としての使い方と、使う意義と目的について考えろ!”代幾”は道具であって便宜だ。使ってナンボだ!」 などということを高校時代の数学の先生に言われたことを思い出します。 当時は解ったような、解んないような感じでしたが、こうしてみるとこれはこれで真理を突いていた言葉だなと改めて思います。
複素数の直交座標系と極座標系
道具と割り切り活用するために、複素数についてもう1歩別の概念についても触れて、計算の省力化をさらに考えます。
複素数の極座標表示
これまでに触れたように複素数を実数軸と虚数軸の2つに分けて表示する方法を「直交座標系」といいます。 実数部分をx、虚数部分をyとすると、x+jyという形で表し、xとyの軸が直交するので直交座標系といいます。
複素数にはこの直交座標系だけではなく「極座標系」という別の表記方法があります。 極座標系では、「原点からの長さ」をr、「実数軸と成す角」をθとおくと、|r|(cosθ + j sinθ) と表されます。 (なお複素数対応の関数電卓などでは極座標表記のr∠θと表記したり、直交座標表記のx+jyのように表示は切り替えられるようになってます)
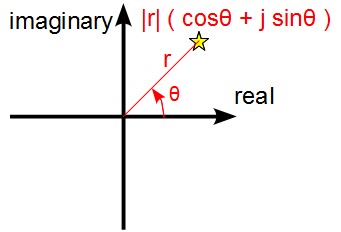
なお、「r」は当然原点からの長さ(半径)を表していますが、0以上の実数値であることを明示するために|r|と表記しています。
複素数とオイラーの公式
ここでオイラーの公式 e^(jθ) = cosθ+ j sinθ という有名なモノを持ち出してみます。
![]()
この式を使って、極座標系で複素数を表示してみると、原点からの長さ=r、x軸(実数軸)からの角度=θの複素数は、
|r| e^(jθ) … (つまり「半径」掛けるeの「jθ」乗)
と、とてもシンプルに表すことができます。eは自然対数の底(ネイピア数)で、jは虚数単位、θは回転角。
それにしてもjθという虚数単位が指数に乗っかっちゃってて「一体何がなにやら」という数式ですが、それは後述。
さてオイラーの公式と極座標系を使って、さっきとまったく同じ「複素数の掛け算」を図に描いてみるとこうなります。 |r|は原点からの距離(正の数)なので、三平方の定理を使って実数部と虚数部それぞれの平方和の平方根です。 それらに「角度」であるeのjθ乗を掛ければこの図の様に各複素数は極座標表示で表せます。
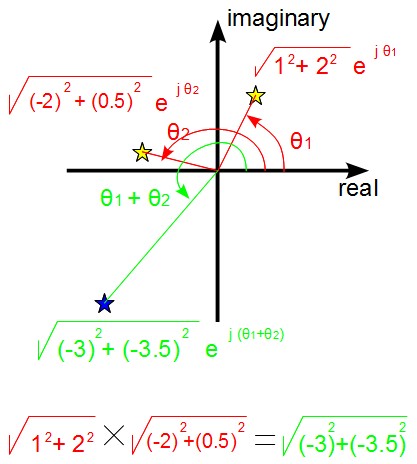
これらは表示方法を変えただけなので、直交座標系でも極座標系でも表しているものはまったく同じ意味なのですが、 極座標系では複素数同士の計算はかなり楽になります。 「回転」という視点で考えれば、極座標表示の掛け算は「長さ」同士の掛け算と「角度」同士の足し算という直感的なカタチで計算することができます。
そして先ほど記したように回転を何度も繰り返すという計算は、複素数で表した値を何度も掛けていくということ(つまり複素数のべき乗)なので、 極座標系で表しておいた方がアタマで考えたり計算したりがラクチンになります。 べき乗計算は指数表示では「指数部の掛け算」という単純な計算で表すことができ、 また半径を「1」にしておけば一定のまま角度だけ変えるのが簡単だからです。たとえば45度ずつグルグル回転していくことを考えてみます。
r ( e ^ (j * 2π/8) ) ^ n
2π/8は45度。それをn乗しているので(45×n)度回転しているという意味になります。この式を整理すると…
r・e ^ (j π n /4)
となり、nが指数部分に掛け算の形で現れるだけ。半径がrのまま、回転角をnの掛け算で表すことが出来ました。
(補足):オイラーの公式について
オイラーの公式…右辺はともかく、左辺は「e」(ネイピア数)の指数部に「複素数」が乗っかってます。どう見ても「なんじゃこりゃ?」です。 言葉を選ばなければ、「変態」以外の何者でもありません。想像上の数の回数だけ掛けるって、なんじゃ?
このように指数部分に複素数が入ったものを「複素指数関数」と言うみたいです。指数部に複素数が乗っかっているのでそう呼ぶみたいです。 正直学生時代に習った記憶がありません。習ったのかも知れないけど、オイラの脳ミソは受け付けた覚えがありません。 複素数が指数に載ってるっていうのは、オイラ含め3次元空間で生活しているヒトでは理解できるって方が変だと思います。(個人の感想です)
ネット上のオイラーの公式を色々彷徨ってみると、数学的に正しい説明や証明が色々書かれているんですが、 数学でジンマシンが出るオイラとしては、オイラーの公式がなぜ成り立つのか、”感覚的に”つかんでみることにします。
で、オイラーの公式の角度変数「θ」に「-θ」を入れてみることにします。
e^(-jθ) = cos(-θ)+ j sin(-θ) …こうなります。
cos関数はθ=0で左右対称、sin関数は原点で点対称の関数なので、cos(-θ)=cosθ、sin(-θ)=-sin(θ)となります。整理すると…
e^(-jθ) = cos(θ)- j sin(θ)
となります。この式とオイラーの公式の両辺をそれぞれ掛け合わせて見ると…
e^(jθ) * e^(-jθ) = (cosθ+ j sinθ) * (cos(θ)- j sin(θ) )
e^(jθ -jθ) = (cosθ)^2 - (j sinθ)^2
e^0 = (cosθ)^2 + (sinθ)^2
1 = 1
となると思うので、なんとなく等式が成り立つことは感覚的に解ります。(厳密な証明ではないので要注意!) まぁ、「数学サイト」じゃないので、感覚的に解ったところまでで留めておきます。(というかこの辺で勘弁ね)
ちなみにオイラーの公式を変形すると、sin関数やcos関数はこんな風に表すことができます。
cos θ = (e^jθ + e^(-jθ)) / 2
sin θ = (e^jθ - e^(-jθ)) / j2





