PIC AVR 工作室->TopPage->資料倉庫->FFT・複素数入門
FFTの計算と複素数の入門
FFTというのは、フーリエ級数を高速に求める計算処理の方法です。応用範囲は広いのに、(少なくともオイラには)取っ付きにくい概念の理解と少々複雑な計算処理の実装をしないといけません。 FFTを計算するプログラムやライブラリは各所で公開されているのですが、実行速度をカリカリにチューンするとか、 自分でFFTのライブラリを新たに組む場合には手を抜かず仕組みから理解しないといけないようです。
で、高校生時代から鬼門にしてきたFFTについて、年取ってからあらためて挑戦してみたところ、なんとか自分の用途レベルでは応用できるレベルまで進むことができたと思うので、 忘れないうちに頭の中のモノを書き出しておきたいと思います。
↑excelシート上で64点FFTを計算させてみた結果です。これを目指します。 (特定のマイコンチップや特定の言語によるプログラムの製作ではなく、EXCELのような表計算ソフトなどによって計算処理の仕組みが解ることをゴールにしました)
なお例によって入門者は私なので、内容的にはそれなりです。あしからず。
はじめに
応用範囲は広いけど、数学苦手なオイラのような感覚人間にはなんだか取っ付きにくいFFT。初めてFFTのことを知ったのは高校生のころ。でも当時は全然理解できず…
まもなくして見つけたのがフーリエの冒険。
とても平易に書かれている本だったんだけど、それでもオイラ程度の頭ではプログラム組めるレベルまでは読解できなかった…(TへT)
それ以後もFFTに関する色んな本を時々パラパラと眺めてみては「はぁ…」とため息。プチトラウマ。所詮オイラには理解できないんだろうなぁ…と。
ところが人間。いざ必要に迫られてみると何とかなるようで…
というわけで、いつものようにオイラがFFTを入門してみて壁になったことについて、どんな壁にブチ当たって、 オイラの視点・脳ミソでどんな風にブチ破ったかを纏めておきたいと思います。
そう。例によって入門者はオイラ。このページを読んだからといってFFTが一から十まで理解できるわけじゃぁありませんが、 「FFTのお勉強はしてみたものの、なんだかよくわからないところがあるんだよなぁ…」という方がきっと感じるであろう「モヤモヤ感」の突破口にはなるかもしれません。
このページの目的は、FFTを理解するうえで躓きそうなところ(オイラが躓いたところ)をピックアップして、どうやって乗り越えたら簡単だろうか…をまとめたページです。 普通の人が読めばもっと躓く箇所は少ないはず。そういう意味ではいろんな人に役に立つのでは?と思うわけです。
ちなみに、私がFFTを自分なりに理解するのに読んだ本はやり直しのための信号数学
の1冊。入門者なので穴が空くほど読み込んだんだけど、高校数学レベルをベースに読み解いていけば充分理解できるレベルでした。なかなか良かった。
多分、学校の教科書でもその他の入門書類でも何でも良いんだと思いますが、コンピュータでプログラム作ることを前提に考えるとこのくらいの盛り込み方がバランス良いんじゃないかな、 という感じでした。
目指すところ
上述のとおり、このページを読んだだけではFFTをゼロから使いこなすことはできませんが、「FFT関係の市販本を読んでみたけど、ココが良く解かんねーだよ」 という方にとっては、「ほぉ、そう考えればよかったのか!」といった具合に役立つのではないかと思います。そんな風に概念的に難解な部分にだけ着目して、 それ以外は市販本で読み進めて頂ければ…と。
特に、FFT関係の入門書類を読んでいてコンガラカッタ人にとって…
- なぜ、たくさんの波が重畳した状態を個々の波に分離できちゃうの?
- なぜ、波(信号)をベクトルで表すの?
- なぜ、複素数を使うの?
とか、
- 正規直交規定って、何?
- オイラーの公式って、何?
- 回転因子って、何?
- DFTとFFTの関係は?
だとか、もしくは…
- 計算で求まったフーリエ級数は、どうやって使うの?
と言った事を一つ一つクリアにしたうえで、実際にプログラムにコーディングできるであろうレベルまで咀嚼していきたいと思います。
ただし、理論的厳密性は求めません(本を読めば書いてあるので)。
躓くところ要所要所で、どんな風に頭を切り替えたのかということ主眼におきます。 なにしろFFTを理解するうえで必要なリクツはせいぜい高校の数学レベルなので、「見方」さえ分かればあとはなんとかなるもんだ…と。
で、このページのゴールですが、本当は実際に何かひとつプログラムを組んでみるといいんだろうと思います。 が、特定の言語に依存するよりもexcelシートにしてしまうほうが色々弄ってみたり、 計算式を眺めたりするのに便利だと思うので、excelシート上に計算式を埋め込み、FFT計算がビジュアル的に理解できるように…ということを念頭に置きます。 こんなexcelシートを作成するのをゴールにしたいと思います。(図をクリックでexcelシートを開きます)
ここまでたどり着けば、どんな言語でもコーディング自体はたいした話じゃないでしょう。ちなみにこの図は64点サンプリングで矩形波をFFT掛けてみたところ。 セルの数値(B列)を書き換えるだけで直にグラフに反映されて面白いので、是非一度弄ってみてください。
私の場合はアセンブラでフルスクラッチしてFFTのライブラリを組もうと思っていたのでゼロから入門したんですが、 高級言語で組むなら既にネット上に転がっているだろうし、大事なのはFFTのロジックを実現することよりもFFTを利用するアプリケーションの方にあると思います。
よほど酔狂なFFTマニアか、私の様に特定チップのアセンブラ用にFFTライブラリを作る必要でも無い限り、FFTのお勉強は必要ないのでは?とも思えますが、 一方で「骨の髄までFFTを使い倒す」ためにはFFTの中身がわかっていないといけないのでは?といえるのではとも思います。
というわけで、「FFTとは何ぞや」レベルを「あえて」纏めておく必要は少なからずあるのではという気もします。
前提知識
上述の通り、FFTを理解するには高校レベルの数学で十分です。しかもそのごく一部しか使いません。「三角関数」「ベクトルとその演算」「複素数」くらいでしょう。
FFTは「波形」に関するジャンルですから、さすがに三角関数について知らないと太刀打ちできそうに無いのは想像に難くないでしょう。 (三角関数については当ページ内では特に解説しません→別途三角関数に関するサイトや参考書をご覧ください)
で、ベクトル演算???なんでベクトルが関係するの?とオイラ的にも最初は思ったんですが…使うんです。解っちゃえば確かに便利なんです。 ベクトルの内積を使います。なぜベクトルを使うのかは後で触れます。(ベクトルとはなんぞや?についてはやはり当ページでは解説しません)
それ以外は小中学生時代の算数・数学で十分だし、複素数については後でザックリ整理します。
波の重ね合わせについて
波とFFT、DFT
FFTというのは、大雑把に言うとたくさん重ね合わさった波を「個々の周波数の波(正弦波)」に分解するためのモノです。
定義を厳格にしようとすると面倒くさくなるので、例によってイメージ図で逃げることにします。
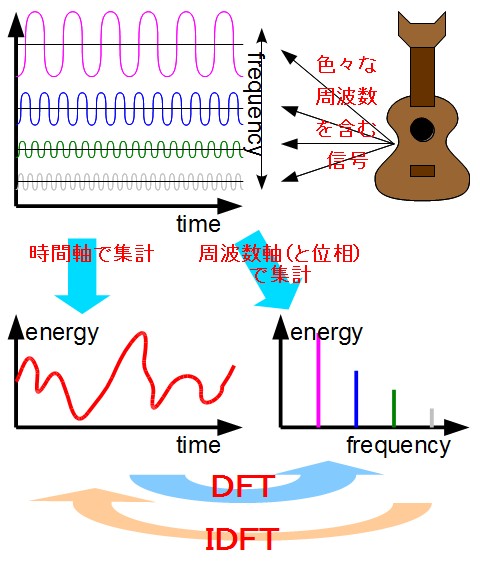
例えば、左上のグラフが色々な周波数の波(元の波)の集まりだとします。仮にウクレレから出た「音の波」だとしましょう。 それを時間軸で集計したもの(左下の赤い曲線)が私たちの耳に届く「音波」というものです。色々な波が重なり合って、こんな風にウネウネしてます。 この音声信号をマイクなどでAD変換掛ければ当然このような赤い曲線のデータが得られるって訳です。
えぇ? 1+2=3 だけど、3は1+2なのか、4-1なのか、1.5+1.5なのか判んないじゃないか! なんで3を1+2に分解できるのさ?って思うのがきっと普通の感覚じゃないでしょうか。その3を1+2と分解するのがFFTなりDFTなどといわれるもの。 不思議なものです。
DFT
この赤い曲線データを図の右側のように各周波数毎に分離して、周波数ごとのエネルギー(スペクトル)を得る計算がDFT(discrete Fourier transformation)で、 逆に周波数領域のデータ(右のスペクトル)から合成した波に戻すのをIDFT(inverse discrete Fourier transformation)といいます。
この「discrete」というのは「離散」という意味です。本来音声などのデータは「連続」しているはずですが、デジタルサンプリングする際には一定時間ごとに標本化する必要があるので、 連続だったデータはコンピュータ内では「離散データ」として扱うことになります。で、離散データを扱うことになるので「DFT」という名前で呼ばれます。
細かく言うと、この図右下のグラフには「位相」や「負の周波数」の概念が出てこないので不正確なんですが、ややこしくなるので省略してます。
DFTとFFTの関係
DFTを高速に処理する計算ロジックをFFT(fast Fourier transformation)といい、IDFTを高速に行う計算ロジックをIFFTといいます。
で、DFTとFFTの関係ってなんでしょう?。
手を抜いて計算時間を短くするのがFFT
昔誰もが聞いたことのある問題に「1~100まで足したらいくつでしょう?」って言うのがありますよね。 この計算を実際に1+2+3+…+100と馬鹿正直に行うのがDFT計算。一方(1+100)+(99+2)+…(50+51)=101×50=5050 のように手を抜くのがFFTというわけです。
理論上はどちらも同じ計算結果が得られますが、データ数が増えれば増えるほど指数計算的に処理時間が増加していくのがDFT計算なので、 一般にはFFT計算を行って処理時間の削減をはかりたくなるのが人情というものです。(実際はもうちょっと複雑ですが)
というわけで、FFTの前にまずはDFTとは何ぞや?について理解する必要があるわけですね。
そのうえで、どのようにして計算の手を抜くことができるかというのがDFT→FFTを理解する筋道になります。 FFTを理解するうえで難しかったのはなんと言ってもDFTを理解するところまでで、それを踏まえてFFTを理解するのは所謂「テクニック」レベルの話。 このページではまずDFT計算の意味についてをメインに進めたいと思います。
改めて、ベクトルの話
ベクトルの特徴
ベクトルについての詳説は省きますが、ザックリとベクトルの特長について整理しておきましょう。
ベクトルの対義語はスカラーで、スカラーというのはいわゆる「普通の数字」のことです。1とか2とか1000とか3.14とか…「大きさ」を表す数値のこと。 で、ベクトルって言うのはこの「大きさ」に加えて「方向」を併せ持つモノ、なんてことを高校で習いました。
その高校の授業では、ベクトルに関する「計算」については「内積」と「外積」について習いました。DFT、FFTでは内積の概念が必要です。 ベクトルの内積については詳説を省くので、ネットで検索するか高校数学の参考書などをご参考ください。
DFTと内積
で、なぜDFTに内積がでてくるのか…。
内積を求めると、同じ方向のベクトル同士ならスカラー値を掛け合わした結果が求まり、方向が直交していれば大きさに関わらずベクトルの大きさはゼロになると習いました。 「aベクトル」と「bベクトル」の内積は、aベクトルの大きさとbベクトルの大きさを掛けて、その成す角の余弦(cos)を掛けて求めるんですね。
言い換えると、ベクトルの内積は各ベクトルの「方向が近いのかそれとも直交に近いのか」を計るのに利用できるわけです。余弦が効いてくるわけ。 二つのベクトルの角度が近いのか、それとも遠いのか、ということを単純な数値演算で求められるわけです。
高校の数学では、ベクトルを表現する次数はせいぜい三次元空間でした。X軸、Y軸、Z軸で表される空間ですね。図に表すとこんな感じ。
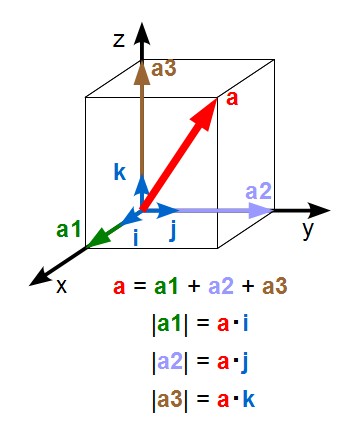
赤く示したベクトル「a」ですが、このベクトルのx成分、y成分、z成分のベクトルをa1ベクトル、a2ベクトル、a3ベクトルとすると、 a1、a2、a3各ベクトルの大きさ(スカラー値)は、各軸の単位ベクトル(i、j、k)を使うと、aベクトルとi、j、k(各単位ベクトル)との内積で図中の式の様に表すことができます。
内積と類似性について
見方を変えると、aベクトルとx軸、y軸、z軸方向の単位ベクトル(図中i、j、kのことで、お互いは直交している)との内積を求めることは、 aベクトルのx、y、zの各成分(大きさ)が求まるということでもありますが、実はこの成分を抽出するということは、各単位ベクトルとの「方向の類似性を数値化」することだったりします。
aベクトルと単位ベクトルが同じ方向を向いているなら内積はaベクトルの大きさそのものになるし、直交しているならゼロになります。 中間的な角度ならaの絶対値とゼロの中間的な値をとります。ベクトルが同じ方向を向いているのかアサッテの方向を向いているのか、 「方向の類似性」を数値化しているわけです。(厳密なことは代数幾何の教科書を読み直してください)
ここまでは内積の復習のお話。これがDFTとどんな関係が有るのか…
ベクトル同士の内積とDFTの関係
類似性とDFT
あるベクトルと各座標軸の単位ベクトル(i、j、k)との内積を求めることによって、各軸方向の成分(大きさ)に分離することができました。
i、j、kのような直交した単位ベクトルとあるベクトルの「内積を求める」ということは、「各軸方向毎の成分の大きさ」を抽出する行為ともいえるわけです。
お、なんか近づいてきた感じがします。
「あるベクトルから各軸方向の成分を抽出する」というのと「ある波形から各周波数の成分を抽出する」、似てますね。
単に言葉が似ているだけじゃなくて、実はこういう計算を行うのがDFTだったりするのです。DFT計算を理解する上でポイントとなる一番大事なことは、実はココ。
ざっくりとDFT
DFTの計算は、各周波数成分の大きさ(成分)を各周波数毎に内積を求めていくことで「波形データと各周波数成分の類似性」を数値化すること。 言い換えれば、「AD変換した波形データ」と、各周波数を意味する「単位ベクトル」との内積を求めていくことによって、「各周波数の成分を数値化」していくこと。 これがDFTのザックリとした考え方です。
大事なことは、「サンプリングしたn個の波形データをn次元のベクトルとして扱う」、「そのベクトルと、各周波数ごとの単位ベクトルの内積を求める」、 「求まった内積の値を各周波数の成分とする」ということ。これがDFTの計算といっても過言ではありません。
例えばさっきの図でいうと、aベクトルはAD変換した3つのサンプリングデータそのもの、iは直流成分を表す単位ベクトル、jは3サンプルで1波形分となる余弦波のベクトル、 kは正弦波のベクトル。で、i、j、kとの内積を求めれば、それぞれ直流成分の大きさ、余弦波成分の大きさ、正弦波成分の大きさが「数値」として求まるわけです。
…なんのこっちゃ? かもしれませんね。すこしずつ整理していきます。
ちょっとタンマ
ちょっとまて、と。i、j、kの各単位ベクトルがたまたまx、y、z軸上にあるから、各単位ベクトルはその成分の一つだけが1で残りはゼロ(例えばiベクトルの成分は(1,0,0)みたいな)。 だからたまたまうまく行ってるんじゃないの?と思ってしまうかもしれませんが…
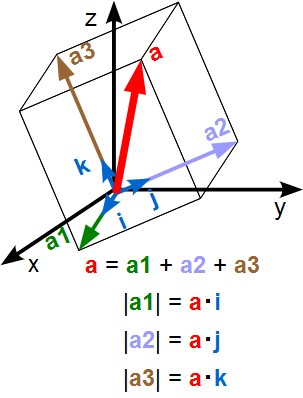
この図の様に各単位ベクトルが斜めになっていたらどうなのよ?と。大丈夫。これでもやはりaベクトルとiベクトルの内積を求めればa1ベクトルの大きさが求まるし、a2、a3も同様。 この辺がベクトルの一つの特徴。というわけで、各単位ベクトルの成分が(1,0,0)とか(0,1,0)みたいに1箇所だけが1で残りがゼロみたいな必要はありません。 必要なのは各々が直交していること。
3点DFTの場合
では実際に、3点DFTを行う場合のことを図にしてみましょう。3点DFTというと「直流」「cos波」「sin波」の3つの要素にしか分けられないのでつまらないんですが、 理解のためってことで。図は上から直流、cos波、sin波。
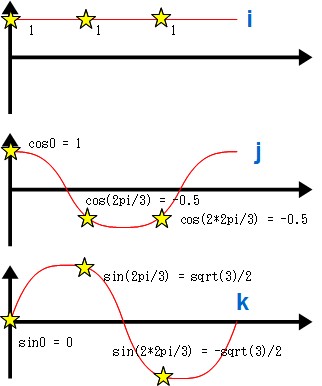
この図みたいに星印のところで3等分して、それぞれの値をi、j、k各ベクトルの要素にしてみます。 するとiとjの内積、iとkの内積、jとkの内積はそれぞれ「ゼロ」になり、i、j、kがお互いに直角に交わっていることが判ります。
これらをグラフにプロットしてみましょう。
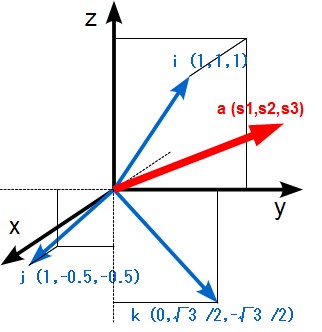
i、j、kはそれぞれ水色のベクトルでこんな位置。仮にAD変換器でサンプリングした3つのデータs1、s2、s3を要素とするaベクトル(図の赤いベクトル)が有るとすると、 DFT変換で求まる直流成分はiとaの内積、cos波はjとaの内積、sin波はkとaの内積ということになります。
まぁ、数学的な厳密さは欠いているので、「だいたいそんな感じ」と思ってください。
ちなみにこれは3点DFTの例ですが、DFTの点数が多くなると星印(サンプルの数)が増えると共に、もっと周波数の高い波までカバーする(i、j、k…とたくさん増える)ようになります。 DFTの点数が増えれば、微妙な周波数の違いまで見分けることができるようになり(周波数分解能が高い)、広い範囲の周波数を扱うことができるようにもなります。
理解が難しいのは、3点DFTなら上図の様に3次元空間に描いて表現できますが、100点DFTなら100次元空間に、1000点DFTなら1000次元空間に思いを馳せないといけません。 3次元空間に住んでる私たちには理解不能の世界ですが、理解できなくても良いんです。必要なのは、100次元なら100個の直交するベクトルを、 1000次元なら1000個の直交するベクトルを用意して、サンプリングしたデータと内積を求めていくことだけ。
試しに6点でDFTを行う場合なら…
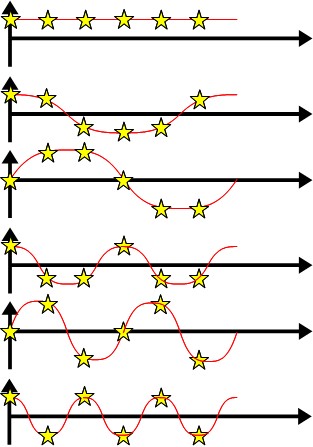
こんな風に6個のベクトルを用意しておいて、サンプリングデータと内積を求めるわけです。なんとなくイメージできたのでは? イメージできると、新たな疑問がいっぱいわいてくると思いますが、とりあえず後々の課題ってことにして先に進みます。 (まぁ、ここまでイメージできれば、後は市販本を読むのはそれほど難しくなくなってきていると思いますが)
さて、ココからちょっと難しくなってきます。各周波数ごとの水色のベクトルをどう扱うか。ここから複素数が登場してきます。複素数って、何?





