PIC AVR 工作室->TopPage->資料倉庫->FFT・複素数入門3
FFTの計算と複素数の入門3
複素数でDFT計算をやってみる
DFTの計算を行ううえで必要なことは一通り出てきたので、これらを元に実際に8点DFTをやってみることにします。
回転因子
「回転因子(twiddle factor)」というモノを持ち出します。まずは”狐がつまむ”ことにして、種明かしは後で。
回転因子「W」というものを以下の様に定義してみます。
![]()
8点DFTの場合、オイラーの公式の「角度部分」を1回転(2π)の1/8にしたものです。 オイラーの公式(の両辺)は極座標で表した「回転」を表していましたから、 何らかの数値(実数でも複素数でも)にこの「W」を掛けると、1周の1/8だけ回転することになります。 複数回掛ければその分グルグル回転するわけです。ちなみに半径は「1」ですね。長さには影響を及ぼさず、回転角だけ変化させることができます。
指数部にマイナスが付いていて、「逆回転」であることを示しています。 私は理由はよく解ってないんですが、FFTやDFTの計算というと、とにかくそういうキマリになっているようです。 ただこの図の様に正弦波を読み込む時のことを考えてみます。古いデータは右にどんどん移動し、 新しいデータが左から入ってくると、正弦波1個を入力したときにこの様にX0からX3には逆位相で収録されます。 このようなことを加味していると考えるとしっくりくると思います。
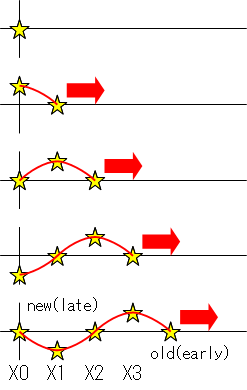
回転因子とDFT
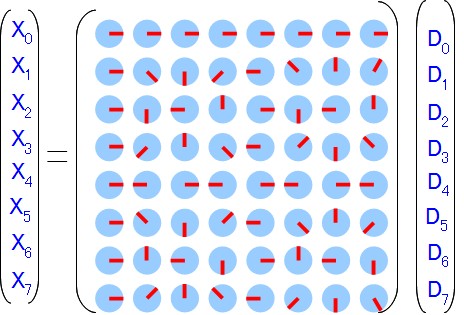
さて、この回転因子「W」を使ってDFTを行うための変換行列を示します。 先ほどsinやcosを使って6×6の回転因子みたいな行列を示しましたが、あれと大体同じものを複素数を使って書いたものです。

右側のD0~D7はADCから取り込んだサンプリングデータ、左のX0~X7はDFTの計算結果で、それぞれこのように8次元の複素数ベクトルになっています。 (ベクトルとか言ってますが、いわゆる8組の配列データで、複素数で実数部と虚数部があるのでそれぞれ8×2=16個の変数だと思ってください)
Wがいっぱい並んだ行列変換の式になっていますが、計算自体は高校時代に習ったことそのままです。例えばX1は…
X1 = W^0・D0 + W^1・D1 + W^2・D2 + … + W^7・D7
といった具合です。昔習ったとおりに「掛けて足す、掛けて足す、掛けて足す…」を8個繰り返すと、X1が求まります。 X0からX7までそれぞれ同じことを行うと、DFTの計算が出来てしまいます。(これらX0~X7の値が何を示すのかは後ほど)
回転因子Wの右肩には指数部が載っていて、それぞれがグルグル回転を表していることが想像できます。 数式だとイメージし難いかもしれないので、変換行列部分をマンガにしてみます。こんなイメージでしょう。
まず上から2段目を見てみます。一番左の水色の丸は赤い線が右向きに出ています。 順に右に1個ずつズレるに伴って1/8回転ずつ回転しているのが判ると思います。 指数部分が1ずつ増えていくので、指数に比例して1/8回転ずつ回っていくわけです。左から右まで8個の丸で1回転分です。
さらに3段目を見てみます。
さっきのWの指数部は2段目と比べて2倍の値になっていて、2倍の角速度となっています。 丸印の中の赤い線の回転速度を見ると、確かに2倍の角速度で回転してることがわかります。左から右までの8個の丸で2回転しています。
以下、1段下がるごとに回転する角速度が3倍、4倍…7倍と増えていきます。ちなみに一番上は回転しておらず、直流成分を表しています。
この回転因子の行列は複素数なので、このようにイメージした方が後々解りやすいかも知れません。

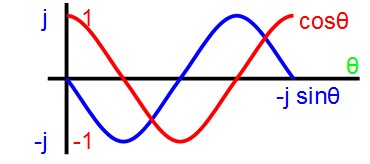
これらの赤い線のx軸が以下のcos曲線(実数)、青い線のx軸が以下の-j・sin曲線(虚数)のイメージ。
DFT計算結果の見方
DFTを掛けてて求まったX0~X7の各値に何が格納されているのかを考えてみます。
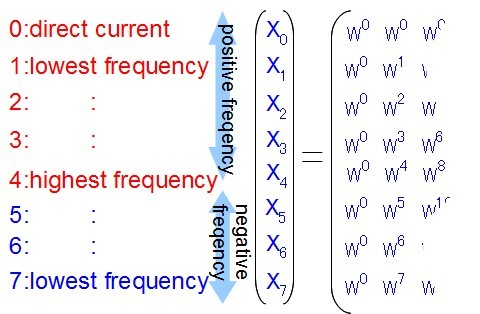
まずX0ですが、ここには直流成分が抽出されます。直流成分は実数部分だけに値が入り、虚数部分には値が乗りません。ここは簡単ですね。
次にX1を見てみます。X1は最も低い周波数成分が抽出されます。8点FFTであれば、ADCのサンプリング周波数の1/8の周波数です。 例えば1秒間に1000回ADCを行うとしたら、1000÷8=125Hzの成分が抽出されます。なお実数部分にはcos成分が、虚数部分にはsin成分が乗ります。
オーディオ機器のグライコの様に「周波数ごとのエネルギー量」を知りたいならcosだのsinだのといった「位相」の情報は必要ないので、 このX1ベクトルの長さ(実数部と虚数部の平方和の平方根)を求めればよいわけです。
X4には最高周波数の成分が入ります。DFTの計算によって抽出できる最高周波数はADC周波数の半分(毎秒1000回のADCを行う場合なら500Hzまで)で、 先ほどの図ではX4が相当します。グライコのような一般用途ではX0~X4までの5個のデータだけ利用し、 X5~X7の3つのデータは捨てられることが多いでしょう。
なお、最高周波数(この場合X4のこと)ではcos成分しか抽出できません。sin成分が仮に乗っていても抽出できないので、 実質的にはこの最高周波数に相当する成分についてはグライコのような用途では利用できないものと考えておいた方が良さそうです。 (そういう場合はサンプル数を増やしたりサンプリング周波数を高く設定するなど見直しが要りそうです)
さらに直流(X0)とそれ以外(X1~X7)では算出された「ベクトルの長さ」の値に少々差異があることに注意が必要です。 X0(直流成分)では計算で求まった値をそのまま適用すればよいのですが、 その他(X1~X7、つまり交流成分)は「正の周波数成分」と「負の周波数成分」に分離して計算されるので、求まった値は半分になっています。
例えば、サンプリング周波数の1/8周波数の成分は、X1(正の周波数)とX7(負の周波数)の2箇所に分離します。 (これらは値を2倍して評価する必要があります…負の周波数については後述します)。
「目指すところ」の章に貼っておいたexcelシートに試しに「直流だけの信号」や「cosだけの信号」を入力してみて、 入力波形と出力結果を比べてみるとそのあたりが実感できると思います。
ちょっと手を抜いてみる
DFTの計算方法と計算結果の見方を示したところで、少しずつ手を抜いていくことを考えることにします。
先ほどのW(回転因子)の行列には指数がたくさん乗っかっています。この例でWは1/8回転を表していました。 ということは、1/8回転が8個分で丁度1回転に相当することになります。
1回転すれば元に戻ることになるわけなので、実際の回転位置は各指数部の数値を8で割った余りと考えても同じことになります。 それを加味して回転因子の行列を8で割った余りに置き換えてみるとこうなります。

8で割った余りなので、指数部分が0~7だけになりました。これで計算しても先ほどのDFT計算と同じ結果が得られます。 同じ結果が得られるのに回転因子の種類が少なくできるなら、回転因子の指数計算をいちいち行う必要も無くて、 個数分だけ予めテーブル化し計算を省くことが可能です。 (一般にDFTの計算というと、このように整理した回転因子の行列を使ったものを指すと思います→FFTはもっと計算を省く方法が使われますが、後述)
さて、この行列をまじまじと眺めてみると…
上から2段目(X1の段)はW^0,W^1,W^2,W^3,W^4,W^5,W^6,W^7となっています。 一方8段目(一番下のX7の段)はW^0,W^7,W^6,W^5,W^4,W^3,W^2,W^1となっています。
比べてみると丁度反対向きになっています。DFTの計算結果は2段目と8段目は周波数自体は同じです。
同様に3段目(X2の段)と7段目(X6の段)、4段目(X3の段)と6段目(X5の段)も反対向きになっていることがわかります。
負の周波数について
このX1とX7、X2とX6、X3とX5はそれぞれ正の周波数と負の周波数の関係になっています。 まぁ感覚的に捉えれば、反対向きの回転と見做すことが出来るわけだから「負の周波数」と呼んでいいかもしれません。
このようにあるサンプリングデータから抽出される周波数成分は、正の周波数分と負の周波数分に分かれて収録されることになります。 DFTを行った結果を利用する際にはこのような特徴を理解しておく必要がありそうです(FFTも同様です)。
なぜ「正の周波数」と「負の周波数」に分かれるのかというと、「複素数表記の回転因子」がその要因になっていると思います。
先ほど「回転計算とDFTのイメージ」の節では、「ベクトルの内積」と「関係性の抽出」という観点で、 sinやcos関数(実数)を使った行列を使って内積を求めることで各周波数のsin波・cos波との類似性を抽出するという考え方に触れました。 この様に実数のcosやsinの波形と類似性を比べるなら、単に内積を取れば似ているか似ていないかを数値化できるわけですが、 回転因子の行列(複素数)とサンプルデータ(便宜上実数)の内積を求める場合は、単純に波形の類似性を求めるというだけではなく、 もう少し複雑なようです。
例によってマンガでごまかします。
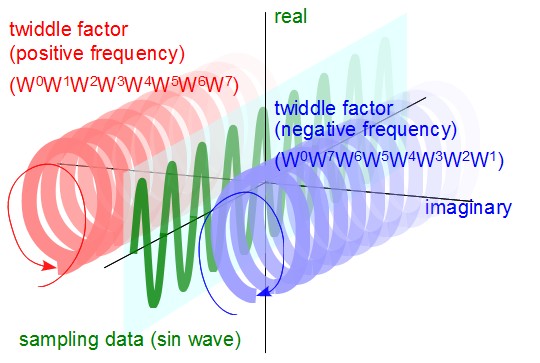
中央にある緑色の波(sin波)を「正の周波数」の回転因子(左側の赤っぽい螺旋)と「負の周波数」の回転因子(右側の青っぽい螺旋)と、 それぞれ内積を取るイメージです。(あくまでイメージなので、回転方向が逆ジャン!とか実数が縦で虚数が横は変だろ! とか8個で一組の回転因子で螺旋1回転分だろ!といった突っ込みはご無用ということで)
この図の赤い螺旋は回転因子行列の上から2番目、青い螺旋は回転因子行列の一番下をイメージしています(同じ周波数だけど方向が正負逆)。
この図の様に、複素数による「回転因子」は複素数空間上に螺旋を描いていて、 一方サンプリングデータ(この例ではsin波)はある「一つの平面上」(実数平面上…図では薄い水色の平面)に存在しています。
「緑の波」と「赤い螺旋」の内積を取れば「X1の虚数部」にsinの成分(の半分)が求まり、 「緑の波」と「青い螺旋」の内積を取れば「X7の虚数部」にやはりsin成分(の半分)が求まるというわけです。
なお、この螺旋状の回転因子は画を描く都合上それぞれ右と左に平行移動して描いていますが、 実際はsin波と中心軸が同じところにあると思ってください。それと、残ったもう一つの軸は「時間軸」だと思って下さい。
cos波の場合も同様にマンガにしてみます。
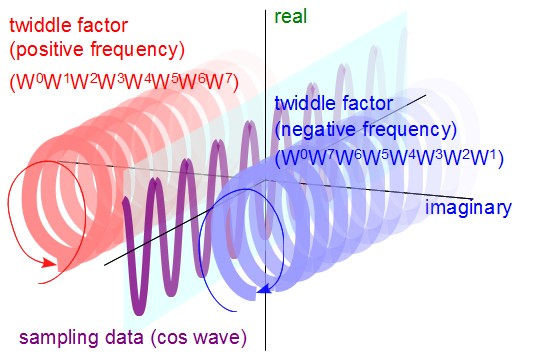
アタリマエですが、cos波も実数軸上の平面にあらわれます。位相が違うので、波の始まりの位置だけ違います。 このcos波は回転因子と内積を取ればsin波とは90度(π/2)だけずれた波形(複素数空間の波形)として相関度合いが求まるわけです。
紫のcos波とそれそれの螺旋の内積を取ってみると、「X1」と「x7」の実数部にcos成分が抽出されます。
そしてアタリマエですが、他の周波数の成分を抽出する場合はこの螺旋の角速度を適宜変えればok。 その該当周波数の成分を抜き出すことが出来るわけです。 回転因子の行列の「Wの指数部分」に着目してみると、 やはりこの角速度のバリエーションをいっぱい用意したものであることが見て取れるわけです。
で、このようにサンプリングデータと回転因子を見比べてみると、実数部分だけに注目してみれば類似性を論じることができ、 その類似性の度合いは「内積を取る」ことで数値化できることについてすでに触れました。
さてこれらのサンプリングデータは、「正の周波数」「負の周波数」どちらの回転因子とも同程度の相関があることはこれらの図から見て取れます。 サンプルデータが実数の平面にしか存在していないので、複素数空間における回転方向は表現できないわけです。
そのため、正の周波数と負の周波数に”同じ程度のの相関が示される”ことになるわけです。
(なお、冒頭のexcelシートを使って色んな位相や周波数の波形にてDFTの計算を行ってみると、 正と負それぞれの成分は同じ値を示すことが判ります…サンプリング波形のエネルギーは、正と負丁度半々に分離抽出されることが実感できます)
ナイキスト周波数とサンプリング定理
さてADCなどを使ってサンプリングを行う際、サンプリングの周波数(毎秒何回サンプリングを行うか:単位はsps(samples per second))と、 サンプル可能なデータの周波数の関係については気になるところです。
サンプリング定理(標本化定理) によると、DFTで周波数を分析できる最大の周波数は、サンプリング(ADC)を行う周波数の半分となります。
例えばコンパクトディスク(CD)を例にしましょう。CDは44100Hzでサンプリングされたデータを収録しています。 この44100Hzでサンプリングされたデータで表現できるのは、その半分の22050Hzということになります。 では、この22050Hzを越える音声信号(いわゆる超音波)はどのようになるのかというと…
簡単な例で考えて見ましょう。サンプリング周波数が5Hz、データとなる信号の波形が6hzという場合を例にとってみます。
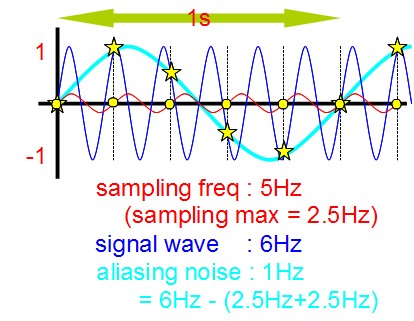
赤い波線が原点に帰るごとに(図の丸印)サンプリングが行われます。この図では毎秒5回。 その時に6Hzの信号(図の青い線)をサンプリングしたとするとどうなるかを表した図です。星印はADC結果の数値で、水色はそれを繋いだ曲線です。
サンプリング周波数が5Hzということは、ナイキスト周波数(サンプリング可能な最大周波数)はその半分の2.5Hzということになります。 信号は6Hzですから、当然2.5Hzを越えているため「正しく」標本化することが出来ません。
このように「扱う信号データ」が「ナイキスト周波数」を超えてしまう場合、元の信号を正しく表現することは出来ず、 「折りたたみ誤差」とか「折りたたみノイズ」などと呼ばれる「ノイズ」が生じることになります。(…aliasing noise)
「折りたたみ」というのは、この図の様に「0Hz」と「ナイキスト周波数」の間で折りたたんだ様にして求まった周波数が「ノイズ」 としてあらわれることに由来します。
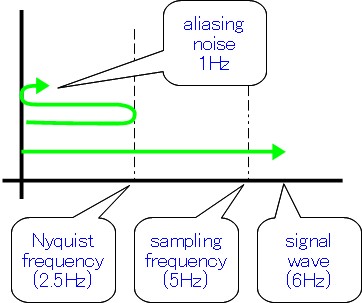
今回の例では、サンプリング周波数=2.5Hzに対して信号は6Hzなので、6Hzの信号がまず2.5Hzで折り返し、さらに0Hzで折り返して、 残った1Hz分だけが生き残って、あたかも「1Hzの信号」としてサンプリングされることになることを示しています。 この様に、0Hzとナイキスト周波数の間で何度も「折り返し」されて「存在しない信号ノイズ」となるので「折り返しノイズ」と呼ばれます。
6Hz - 2.5Hz - 2.5Hz = 1Hz
FFTを掛けるとか掛けないとかに関わらず、ADCからサンプリングを行う際には、 その信号の各周波数成分はナイキスト周波数よりも低くなっている必要があります。 ナイキスト周波数を越える成分はこの様に折り返しノイズという形で存在しない信号に化けて取り込まれてしまいます。
一般には、ナイキスト周波数(=サンプリング周波数の半分)よりも高い周波数成分をLPF(low pass filter) によって削り落とした状態でADCを掛けるのが正しいやり方とされています。 LPFは、ADCで入力する前にオペアンプを用いてアクティブフィルター回路を組むのが一般的でしょう。 例えばCDなら、LPFのカットオフ周波数を22050Hzよりも少し低めに設定し、 それより高周波の成分をカットしてからCD用のデジタル音声データとして収録します。
正規直交基底
さて、「回転因子W」とか「Wの指数表示による行列変換」といったものがなんなのかという説明を省いたまま、 DFTはこうすれば計算できる…と煙に巻いてきました。この回転因子の行列についてもう少し補足します。
回転因子Wの行列は複素数空間で螺旋構造をしたものであることについては既に触れました。
さてこの螺旋を、回転因子の行列を構成するWの指数部分に注目してみると、 一番上から一段ずつ下に下っていくにつれて回転の速度(角速度)が2倍、3倍、4倍…と速くなっていきました。 当然サンプリング数を100点、1000点…と増やしていけば、それだけ細かい周波数分解能によって各周波数の成分を抽出することが出来るようになります。
角速度にこの様にバリエーションを設け、色々な角速度の回転因子とサンプリングデータの内積を取ることで、 その角速度に該当する波の成分を抽出することがこの「回転因子の行列…Wの指数表示の行列」だったわけです。 この行列は複素数空間に螺旋を描いているので、サンプリングデータ(実数空間)と内積を取れば、 各周波数のcos成分・sin成分がそれぞれ実数部・虚数部に現れ、抽出することが可能です。 で、この行列の一行一行と内積を取ってみると、実際に各周波数の成分に毎に分離できます。
また、この角速度がナイキスト周波数に達するまでは「正の周波数」の螺旋として、 ナイキスト周波数を越えたところからは「負の周波数」の螺旋として、それぞれ機能することについても触れました。 (8点DFTであれば、1番上の段が直流、2番目から5番目が正の周波数、6番目から8番目までが負の周波数でした)
DFTはこの様に、回転因子の行列に複数の周波数にあたる複素数の螺旋を格納しておいて、 それらとサンプリングデータの内積を取ることで各周波数成分に分離することができます。
ここで、この回転因子の行列一行一行の関係性について「正規直交基底」という観点に触れておきます。
「正規」というのは、ベクトルの長さを「1」にそろえるということを示しています。 複素数ベクトルの「直交座標系」と「極座標系」について触れた際、ベクトルの長さについても触れました。 長さが1のベクトルの場合、何回掛けても長さには影響せず、指数表示によって回転角だけを操作することが出来ました。 長さが1だから何回掛けても長さには影響が無かったわけです。 回転因子の行列の各要素に「W=e^(-j2π/n)」の様に半径1のベクトルを用いたのは正規化のためです。
次に「直交」という概念について。ベクトルは、直角に交わったベクトル同士で内積を求めるとその値は「ゼロ」になります。 ページのアタマのほうでは、3次元空間上で直角に交わった3つのベクトルのお互いがそれぞれ直角に交わっている様子について触れました。 3次元に限らず、どんな次元のベクトルでも直角のベクトル同士の内積はゼロになります。
先ほどの8点DFTにおける回転因子の行列で、上から順に1段ずつ切り出してそれぞれを1組のベクトルとしてみます。
一番上は(w^0,w^0,w^0,w^0,w^0,w^0,w^0,w^0)で、2番目は(w^0,w^1,w^2,w^3,w^4,w^5,w^6,w^7)、 …7番目は(w^0,w^7,w^6,w^5,w^4,w^3,w^2,w^1)といった具合になっています。
これら8個の中から任意の2つのベクトルを取り出して内積を取ってみると、すべての組み合わせで内積が「ゼロ」になることがわかります。 (ご興味のある方は実際に計算してみてください…特に正と負の周波数同士も内積を取ればゼロになっているのは面白いところです)
内積がゼロということは、それぞれのベクトルが直角に交わっていることを表しています。 Wの指数形式で表した回転因子の行列は、指数部分が規則的に並んだ感じになっていましたが、 実はこの様に直角に交わるようになっていました。
直交しているということは、言い換えれば各周波数のベクトルが「お互いに独立(一次独立)である」ことを表しています。 DFTでは、お互い独立した「各周波数」に分離(周波数毎の成分を抽出)したいわけなので、 この様にお互いが直交したベクトルで構成するわけです。
整理すると、「内積=0」→「直交している」→「独立した各周波数成分に分離できる」ということです。
基底というのは、数学的な定義は端折りますがこのようなベクトルの集まりのことで、 「長さが1」「直交している」ので、回転因子の行列は「正規直交基底」となります。
実際に数字を入れてDFT計算
リクツっぽいことは一通り触れたので、実際に数字を当てはめて計算をしてみることにします。
4点DFTで計算してみる
出来るだけ簡単に、かつこれまで触れたリクツを盛り込んで計算をしてみるための最小スペックとして、4点DFTをやってみることにします。 まず4点DFTなので、4×4の回転因子を使った行列変換式が登場します。こんな感じ。
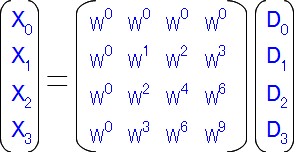
一番上は直流、2番目は90度ずつの回転、3番目は180度ずつ(=最高周波数)、4番目は負の周波数です。 例によって、2π毎に1周して元に戻るわけだから、4点DFTなら4で割った余りの行列にします。こんな感じ。

この場合の回転因子Wは4点DFTなのでこうなります。
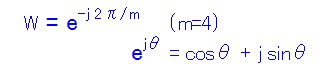
さて、4点DFTだとW^0~W^3はそれぞれこうなります。
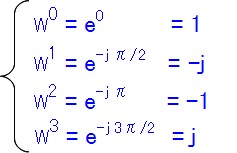
90度単位で回転するのでこのように1、-j、-1、j(実数か純虚数だけ)のように簡単な数値しか出てきませんが、 もっと点数が多いDFTでもさっきの「e^(jθ)=cosθ+jsinθ」の式によってて実数部と虚数部が混在する小さな回転角による 「微小な回転」も同様に計算可能です。念のため。
DFTに入力する波形データ
サンプルデータとして、cos波、sin波、直流が適当に混ざったこんなグラフを元にDFTの計算をしてみましょう。
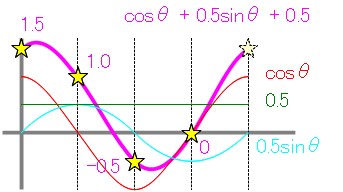
細い線の赤がcosθ、水色が0.5sinθ、緑が直流成分で=0.5、太い線の紫がその合成波「cosθ + 0.5sinθ + 0.5」です。 純粋なcos波と比べると、位相が少し進んだ波形となっています。 星印のところが実際のサンプリング個所で、サンプリングデータは左から順に1.5、1.0、-0.5、0.0となります。 これらの4点をDFTに掛けてみることにします。
計算してみる
先ほどの回転因子の行列とデータを加味すると…

こうなります。で、この行列変換の式を計算してみると…

となり、整理すると…

DFTの結果は直流が2.0、1倍周波数が2.0-j、2倍周波数が0、負の1倍周波数が2.0+jとなりました。 各数値の意味はこうです。
計算結果の見方
X0の 2.0 … そのまま直流が2.0
X1の 2.0-j … 2cosθ -jsinθ
X2の 0.0 … 0cos(2θ)
X3の 2.0+j … 2cos(-θ) +jsin(-θ)
(なお、θは360度÷DFT点数…この場合360÷4=90度=π/2で、例えばサンプリング周波数が1000Hz(1000sps)だとすると、 このπ/2は1000÷4=250Hzに相当)
この結果をcos成分、sin成分、直流成分について正の周波数、負の周波数を加味して集計すると、「4cosθ-2sinθ+2.0」と読み替えることが出来ます。 元のデータは「cosθ + 0.5sinθ + 0.5」なので、比べると各周波数の成分が丁度「4倍の値の波形」として抽出されたことが判ります。
(ただし先ほどもふれたように回転因子W=e^(-j2π/m)と逆回転(指数部がマイナス)に定義されているので、 sin波については位相が逆に抽出されます)。
なお4倍の値になったのは「4点DFT」だからで、8点DFTなら8倍、100点なら100倍、 1000点DFTなら1000倍の値として抽出されます…詳しくはFFTのところで改めて。
補足
今回サンプリングデータとして使用したのは、cosθやsinθのように、サンプリング周波数に対して整数比の角速度のデータでした。 もし整数比ではない角速度の波形を入力したらどうなるのか?
例えばθよりも少し遅い波形(直流とθの中間)をDFT掛けるとどうなるかというと、直流とθの両方に分かれて抽出されます。 θより少し速い波形(θと2θの中間)であれば、θと2θの両方に分かれて抽出されます。
この様に、DFTで計算される各周波数に対してぴったりではない周波数成分のデータも、その近くの周波数に分かれて抽出できるわけです。 言い換えれば、データの周波数に近い回転因子の螺旋と類似性が高いということです。
ちなみに、ぴったりの周波数の場合はその周波数成分として抽出されてしっくり来てめでたしめでたしにになります。 一方、ぴったりではない場合はその両側2つのDFT値に高い相関が現れますが、この両側2つだけにキレイに分かれるのではなく、 それ以外の周辺の周波数にも少しずつ相関が現れます。データの両端を無理やり繋いで周期的に現れるデータであるとみなすため、 取り込んだデータの周波数と実際の信号の周波数に差異が生じる様です。
このあたりは、「窓関数」にからむ話なので、機会があればふれることにします。
改めて複素数
というわけで、計算の仕組みは結構簡単だったり、点数が少ないDFTならあっという間に計算が終わっちゃうことが一目瞭然なんですが、 複素数の計算は少々扱いが面倒です。excelのセルの値や普通のコンピュータ言語の変数では扱うことが出来ません。
処理言語系によっては複素数型の変数やその演算子を実装しているものもあるので、そういうものを使うならラクチンなんですが、 このページのゴールはexcelシート上でFFTを行うこと…excelは複素数を直接扱えません。
それを踏まえて、実数しか扱えない一般的な処理言語系(excel含む)でも複素数が扱えるように考えてみます。 まぁ、実数部、虚数部に分けて2つの変数で管理すればよい、ということは簡単に想像出来ると思います。 足し算・引き算なら実数部と虚数部のそれぞれについて足し引きすれば済む簡単な話です。
問題は掛け算と割り算です。(今回は割り算は使わないんですが、一応補足しておくと複素数の割り算は掛け算と逆方向の回転を表します)
複素数の掛け算(割り算)では、実数部同士の掛け算、虚数部同士の掛け算…みたいな簡単な計算だけでは済みません。 中学校時代に習った、以下のような「カッコの展開」を思い出してください。
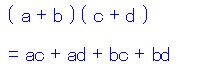
複素数はこのカッコ内のイメージで言うと、aとcが実数部、bとdが虚数部というイメージになっています。 複素数の内積はこのカッコの展開を行うことと同じイメージです。この計算式に、虚数単位「j」を含めて考えてみましょう。
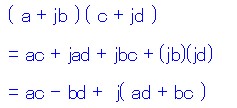
この様に、複素数の内積の実数部は「実数部と実数部の積」から「虚数部と虚数部の積」を引いたものとなり、 虚数部は「実数部と虚数部の積」と「虚数部と実数部の積」の和で表されます。当然、実数部分がcos成分、虚数部分がsin成分です。
さっきの
などはそのいい例です。
excelだろうが各種コンピュータ言語だろうが、この様に「複素数の内積」ときたら「カッコの展開」をやればいいわけです。 excelなら入力値の「実数部と虚数部」の両セルを設けておいて、計算結果が入るセルでは、実数部は実数部の計算式(ac-bd)を、 虚数部は虚数部の計算式(ad+bc)を計算するような式を組んでおけばよいでしょう。 また各種コンピュータ言語では、内積を計算するサブルーチンを組んで使いまわすとよいでしょう。
複素数の掛け算という範疇においては、例えば回転因子の指数計算も含めて、 掛け算ならすべてこのような「カッコの展開」を考えればよいわけです。
少々面倒な計算に見えますが、複素数の概念を使わずにDFT(もしくはFFT)を計算するよりははるかに簡単なはずです。





