PIC AVR 工作室->TopPage->資料倉庫->FFT・複素数入門5
FFTの計算と複素数の入門5
周波数間引きFFT
周波数間引きの考え方
先ほど触れたFFTの計算は「時間間引き」と呼ばれる方法でした。時間軸方向で計算式をシャッフルすることからこう呼ばれるようです。
似たような方法として周波数方向でシャッフルする「周波数間引き」という方法があります。
周波数間引きでは、

この様に縦に1列おきに振り分けて分割していきます。
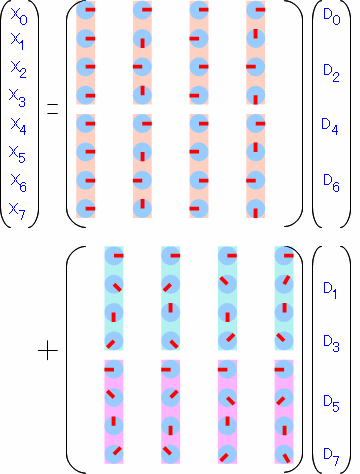
周波数間引きの計算式とバタフライ演算
計算の過程はひとまず端折り、バタフライ演算のフローとその元の計算式だけ挙げます。
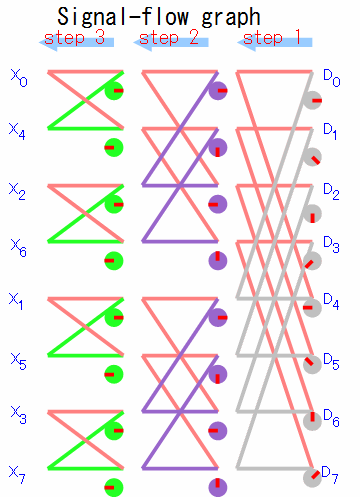

時間間引きと周波数間引きでは、バタフライ演算のフローがおよそ左右反対向きになっていることがわかります。 一つだけサンプルとして取り出してみましょう。
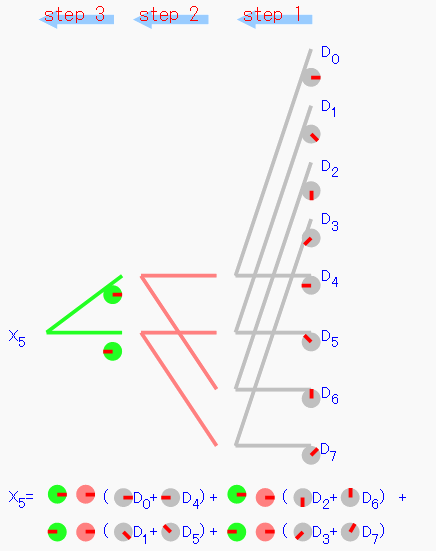
やはり計算式とマッチしています。
時間間引き、周波数間引き、どちらの方式で計算をしても結果は同じになります。 DFTの回転因子行列からFFT計算を導き出すのは時間間引きの方がわかりやすいような気がしますが(個人の感想です)、 どちらもビットリバーサルという並べ替えの処理が必要になり、個人的には周波数間引きの方が使いやすいと思います。
(ビットリバーサルについてはあとで触れます)
使いやすいと思う理由について。ADCからの入力データをビットリバーサル処理してからFFTかけるのが時間間引き、 FFT計算後の値にビットリバーサル処理するのが周波数間引き。入力値に一律すべてビットリバーサル処理しなければならない時間間引きに対し、 周波数間引きはFFT計算結果のうち読み出し時に必要なデータだけをビットリバーサル処理すればいいからです。 (必要が無ければ省くことが出来る)
計算量を考える
さて、時間間引きFFTの説明のところで「掛け算の量をさらに減らす」という部分を後回しにしていました。 バタフライ演算の図を眺めてみると、丸印(=回転因子)の向きに規則性があることがわかります。 そこに着目して複素数掛け算の回数を減らすことを考えてみます。
回転因子の「W」について改めて整理します。回転因子Wは8点DFTならW=e^(2π/8)、同様に4点DFTならe^(2π/4)という具合に、 DFTに掛けるデータ点数によって角度2πを点数で割った値になっています。 ただ「W」とだけ書くとデータ点数が区別付かないので、一般的な表記に従って回転因子は以後以下の様に書くことにします。
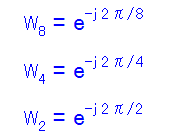
W8は8点、W4は4点、W2は2点のDFT用回転因子を表しています。
これを使ってバタフライ演算の図の丸印を表してみると、
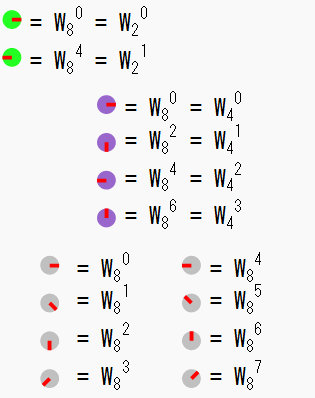
このような式で表せます。なお例えばW4^1はW8^2と同じで-90度の回転を表していますが、何らかの言語でプログラムを組む際には、 このように90度ずつ回転するというような場合に「45度を2個分ずつ回転する(W8^2)」とするより「90度ずつ回転する(W4^1)」 と書いたほうがわかりやすくなると思うので、このような場合は以後W4の方を使うことにします(他の回転因子についても同様)。
さて緑色の丸をみてみると全部で2種類あり、それぞれ反対向きになっています。 右向きは0度の回転で数値でいうと「1」、左向きは-180度の回転で数値では「-1」を表しているので、 緑色の計算は単純に足し算と引き算だけで表すことができます。つまり、この緑色の計算は8個全部の掛け算を端折ることができます。
次に紫色を見てみます。右向きと左向きは「1」と「-1」を表しているので、これらも足し算と引き算で表すことができます。 つまり8個のうち4個は掛け算が端折れます。また上2つ(右向き、下向き)と下2つ(左向き、上向き)はそれぞれ反対方向を向いているので、 下2つの回転計算は上2つと同じ計算を行ってから引き算することで表すことができ、計算処理を共通化できます。
続いて灰色も見てみます。やはり右向きと左向きは「1」と「-1」なので足し算と引き算だけで済ますことができます。 また、上4つと下4つは逆向きになっているので、下4つの計算は上4つと同じ計算を行ってから引き算することで表せます。 噛み砕けばこんな感じです↓。
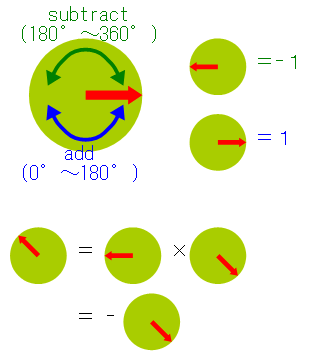
-225度の回転であれば、-180度と-45度の組み合わせなので、-45度の回転をしてから引き算すれば同じ結果になるわけです。
それらを加味して周波数間引きFFTのバタフライ演算を描き直してみます。
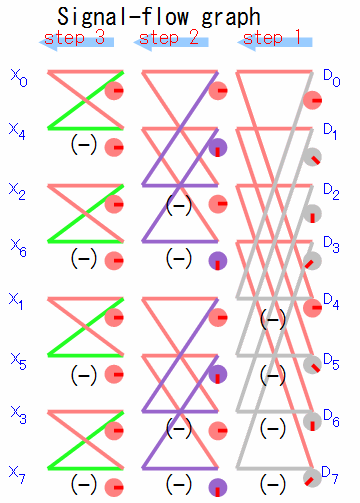
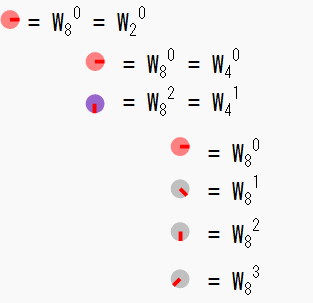
緑色の丸だった部分は足し算と引き算で書き直すことができ、紫の丸も下向きのものだけしか残らず、灰色の丸も右下、下、左下だけが残ります。 この様に減らしていくと、8点FFT全体では複素数掛け算を10回まで減らせることが判ります(紫と灰色の丸の数)。 さらに各回転因子Wのテーブルもそれぞれ半分(180度分)だけ用意しておけば済み、メモリ使用量を減らすことができます。
(注:ただし、例のexcelシートの計算式は、 このような「右向き」「左向き」の回転因子を加減算だけでなく回転計算(複素数でいう掛け算)を行った形で計算しています…理由は後ほど)
バタフライ1個の計算方法、詳細
このようにして掛け算の計算を減らしたバタフライ1個だけを取り出してみて、 具体的にどのようにコンピュータに計算をさせればいいか(特に複素数型の変数を持たない処理言語系:excel含む)を考えていきます。
バタフライ演算から蝶々を1匹拝借
先ほどのバタフライ演算の図から蝶々を1匹捕まえて眺めてみます。step2のX5、X7の段の部分の蝶々です。
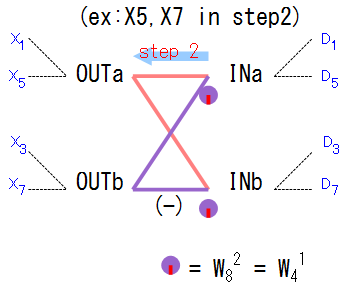
バタフライ演算1個は、このように入力が2個、出力が2個となる計算を行います。
周波数間引きの場合、この図のサーモンピンクの二本の線は単純な足し算を、 それ以外の色(この図では紫)の線は回転因子による回転計算を行ってさらにこの図のようにマイナス「(-)」が書かれている方の線(下側の水平の線) は引き算を、斜めの線は足し算を行います。
この図で言うと、「OUTa」に繋がっているのは両方ともサーモンピンクの線なので「INa」と「INb」を単純に足し算したもの。 「OUTb」は両方紫の線なので回転計算を行います。「INa」を「-90度」回転させたものから「INb」を「-90度」回転させたものを引いた値になります。 このバタフライ演算を計算式で書くとこうなります。
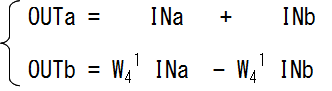
さて、上の式は足し算なので、実数部は実数部同士で、虚数部は虚数部同士で足し算すればいいので簡単なのですが、 下の式は掛け算が登場します。複素数の掛け算はこのように都度「括弧の展開」を行う必要があり、ちょっと厄介なのでした。

(この赤いaとcは実数部、青いbとdは虚数部、jは虚数単位)
複素数型の変数が実装されていない言語系などでは、これらの値を実数部と虚数部に分けて上の式のようにカッコを開く計算が必要です。 で、右辺に登場する「INa」「INb」「W4^1」について以下のように実数部と虚数部に分けて扱うことを考えてみます。

すると先ほどの下の式の左半分(W4^1×INa)のところは実数部と虚数部を分けてこのように書くことができます。

同様に、右半分(W4^1×INb)のところもこのように書くことができます。
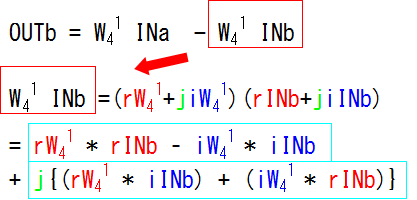
よって、「OUTb」はこのようになります。

これを実数部は実数部で、虚数部は虚数部で纏めてみると…
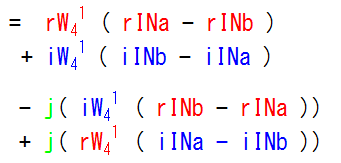
このように整理することができました。
さて、4点DFTの回転因子の実数部(rW4)および虚数部(iW4)はオイラーの公式を使うとその実数部(cos)と虚数部(sin)にあたるわけなので、 cos、sinを使って以下のようにあらわすことができます。(ちなみに逆回転なので例によってsinはマイナス)
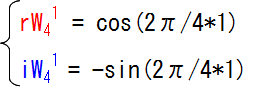
これを代入してみると、

こうなります。
バタフライ計算1個分のうち下半分はこのような計算を行うことで、実数型だけの処理言語系でも扱うことが可能になります。 バタフライ演算のどれを取り出しても、基本はこの計算式です。(もちろん回転角はグルグル変わりますが)
バタフライ演算の式を一般化してみる
8点DFTの2step目からX5、X7のところの計算方法を抜き出して整理してみました。 これを各stepの任意のバタフライ演算に応用できるように一般化してみます。

このような計算式で表すことができます。
ここで現れる虚数単位「j」は実数部と虚数部を分けるための意味で書いてあるので、 実際はj自体は無視して、実装の際には実数部は実数部用の変数で、虚数部は虚数部用の変数で計算すればokです。
さてこの式に「m」「p」という2つの変数がでてきました。これらについて補足します。
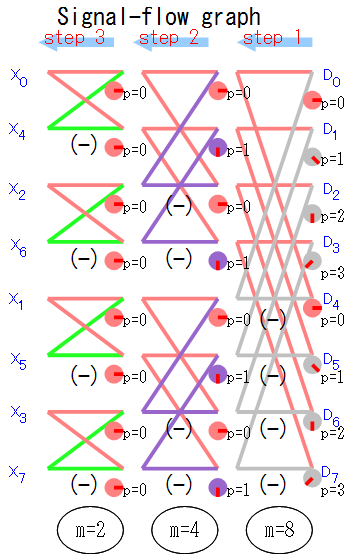
「m」は使用する回転因子のDFT点数を表し、1step目(一番右の列)のm=8は8点DFT用の回転因子W8を使うことを意味します。 同様に2step目の「m=4」は4点DFT用の回転因子W4を、3step目の「m=2」は2点DFTの回転因子W2を意味します。
「p」は、回転因子の指数部を意味します。たとえば1step目なら上から順に「p=0」「p=1」「p=2」「p=3」となっていていますが、 8点DFTの回転は-45度ずつなので、それぞれ0度、-45度、-90度、-135度をあらわしていることがわかります。(もちろん実際は「弧度法」表示ですが)
FFTの1step目では、「rINa」「rINb」はADCからの入力した該当箇所のデータ、「iINa」「iINb」には共にゼロを指定しておき、 先ほどの一般化したバタフライ演算の式4つ分を計算し、それらを元の入力データの配列に書き戻します。 それらの値は後続のstep2、step3へと引き継がれていきます。
これで、大抵の処理言語系でプログラムコードに落とせるレベルまで整理できたのではないかと思います。
(ちなみに同じバタフライ演算のフローでも、時間間引きの場合は流れが微妙に変わってきますが、 周波数間引きと同様に掛け算は10回まで減らすことができ、 回転計算の半分は引き算にすることで回転計算のバリエーションを減らせるといったことは同様です)
8点DFTを選んだ理由
さて、このように「半分、半分、半分…」と次数を下げていくことで計算量を減らしていくのがFFTなわけですが、 半分、半分…と続けて分けていくことができるためには、データ数が2の指数乗になっている必要があります。例えば4、8、16、32、64…など。
今回8点DFTを選んだのは、このように2の指数乗になっている必要があるからで、 その中でもできるだけ描く手間の都合「少なめ」かつ計算式を「一般化して理解できる」データ量として8点DFTを取り上げました。
FFT(Cooley-Tukey型の時間間引き、周波数間引きFFT含む)ではこのように2の指数乗個のデータによるFFTを行うのが一般的ですが、 要はデータ数が小さいDFTに分解していくということが肝要で、それは2点DFTに分解しなくても、3点DFTなどに分解するという手もあるはずです。 (このあたりの「実装時の検討事項」は後述)





