PIC AVR 工作室->TopPage->資料倉庫->FFT・複素数入門4
FFTの計算と複素数の入門4
DFTからFFTへ
DFTを行う上で必要なリクツや、実際の計算方法、計算過程について一通り書き纏めました。 これまで書いたことの規模を大きくしていけば、100点だろうと1000点だろうといくらでも点数を増やしたDFTを行うことは可能です。
ですが、現実的にはDFTの点数を増やしていくと、その計算量は指数関数的に増加して行き、計算時間の点で非現実的になってしまいます。
点数を増やしても処理時間を現実的な範囲に収める為に考えられたのがFFT(Fast Fourier Transform)で、 n点DFTでは複素数の掛け算だけでもn^2回レベル行う必要がありますが、n点FFTではn×log2(n)回レベルで済みます。 (なお、n^2もn×log2(n)も正確な数字ではなく、このくらいの次元の数になるという意味です)
少ない点数ではDFTとFFTの計算量はあまり差がありませんが、点数が多くなればなるほど指数関数的に計算量を減らすことができ、 処理時間的に有利になります。
計算結果はDFTもFFTも同じものが得られますが、計算数が少ないFFTの方が実用上有利であることはいうまでもありません。 FFTの計算式の導き出し方について整理していきます。
基本的な考え方
DFTの計算量を減らす方法の論文を書いたのはクーリーさんとチューキーさんという人で、この人たちの「Cooley-Tukey型FFTアルゴリズム」 というものについて整理していきます。(他にも色々な方法があるようです)
「Cooley-Tukey型FFTアルゴリズム」は、ざっくりとした方向性としては大量の計算の中から共通した部分を抽出し、 その共通部分の計算を1回だけで済ますことで全体の計算量を減らします。
以前ふれたように、例えば「1~100まで足し算したらいくつになるか」という計算では、1と100、2と99、3と98… をそれぞれ足すとそれぞれが101になり、それらが全部で50組存在するから全体では101×50=5050になる、というような計算を行います。 「Cooley-Tukey型FFTアルゴリズム」ではこの「足して101」に相当するような部分がどこにあるのか探して、それらを1回の処理で済ます… みたいな事を多段階で行うことで、DFTの次元数を減らしていきます。
DFTの次数が上がれば上がるほど(FFTに掛けるサンプルデータ点数が多ければ多いほど)計算量が指数関数的に増えていくのであれば、 逆に次数が減れば減るほど指数関数的に減っていくというわけです。
この時点ではまだ「なにがなにやら…」でかまいません。ちょっとずつ整理していきます。
あらためて行列について整理
改めて行列の計算について整理しておきたいと思います。
高校時代、行列とは何ぞや?ということを習いました。DFTでは複素数を扱いますが、「基本は高校で習った行列」そのままです。
なのでその行列について復習しておきます。例えば、このような4元1次方程式があるとします。
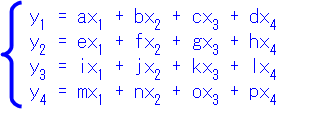
このようなたくさんの変数が現れる式を簡単な操作で扱えるように、行列というものを使って以下の様に表すということを習いました。

つまり、主題にしたい変数「x」や「y」と、それを計算するための係数「a」~「p」を分離して、 ちょっとグラフィカルに書いたものが行列というものでした。
この方程式に現れるx1~x4がADCからの入力データ、y1~y4がDFTの計算結果、a~pが回転因子のWをべき乗したもの。 4点DFTの行列の計算であればこのような4×4次の行列を用いた変換式そのものなわけです。
さて、この行列はご覧の通り4×4の4次の行列です。仮にこの行列が表す1番目・3番目および2番目・4番目の式に分離すると…
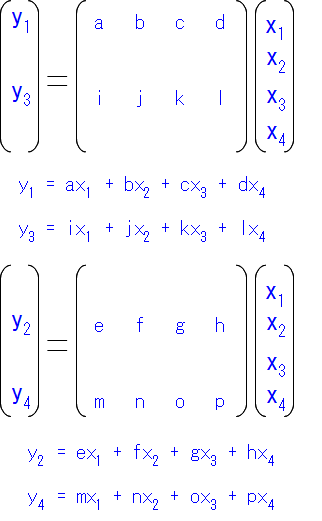
このように表すこともできます。
さらにもし、上の行列計算の左半分と右半分がこんな感じに「一定の比率で関係性(この場合左右がv対wの比率)」が有ったなら…
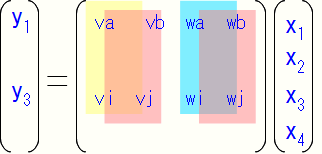
共通部分を括り出すことで、こんな感じ↓に変形することが出来ます。
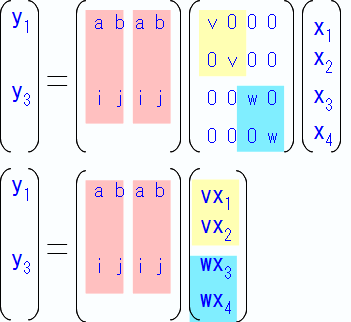
この行列は方程式に戻すと↓こういう意味になります。さてここでa、b、i、jは左右で共通なので、 共通項である「a、b」「i、j」で括ると下の式の様に纏めることができます。
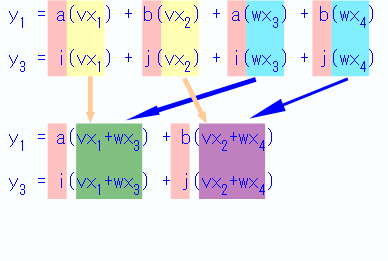
これらの式を改めて行列を使って書き表すと…
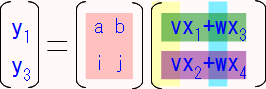
この様に2×2の行列で表すことができます。同様にy2、y4も「t」「u」という比率で表されると仮定すると…
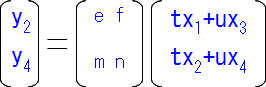
この様に書き表すことが出来ます。「a、b、i、j」や「e、f、m、n」といった共通部分が先ほどの「足して101」に相当するわけです。
さて良くみてみると、元の行列が4×4次元であるのに比べ、この式は2×2次元の式が2つになっています。 DFT→FFTでは、このような変形を段階的に行うことで次数を下げて計算量を少なくして行きます。4点DFTであれば、4×4=16回の掛け算が要りますが、 2個の2点DFTに分解すれば2×2×2=8回の掛け算で済ますことが出来ます(実はもっと少ない回数で済むのですが、詳しくは後述)。 当然もっと多いデータ数の場合では減らせる計算の量はもっと劇的になります。
以後このような行列の基本的な変形が多々現れます。今後は行列の計算だけ表示して方程式は省くので、 わからなくなったら行列を展開して方程式の形で眺めてみてください。
(もしこのような行列の計算でわからなくなってしまった場合は、 適宜行列関係の解説をしてくれているネット上のサイトを探してみてください…時間が取れれば改めて補記します)
時間間引きによる8点FFTの計算
前のページ で出てきた8×8の回転因子行列による8点DFT…

このDFT計算を元に、「時間間引き」という方法で8点FFT計算に変形していきます。(何故8点なのかは後で種明かしします)
8点DFTから共通部分を見つけ出してみる
まず、私のアタマでも理解しやすいように、回転因子Wの「指数表示」の代わりに、例によってマンガ表示にして、着色してみます。
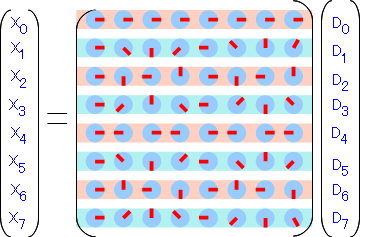
1行ごとにサーモンピンクと水色で色分けしてあります。これらの色毎に2つの式に分解してみます。 まずはサーモンピンクの部分(添え字が偶数の列)を取り出したのがこれ↓。
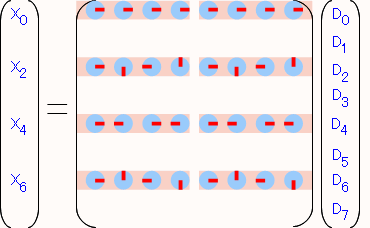
この行列の左右を見比べてみると、まったく同じ形をしていることがわかります。 この様に左右が同じ形をしているのであれば、以下の様に左右の共通項である「右矢印」の回転因子を括り出して…
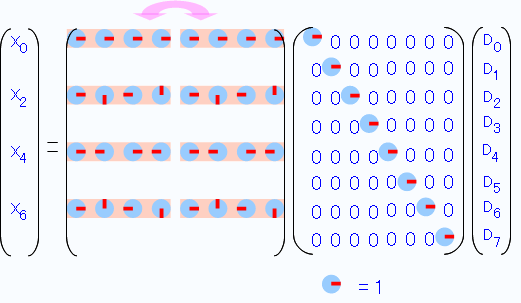
右側の行列だけ先に計算してしまうと↓こうなります。
まぁ、「右矢印」は数値で言うと「1」だから、単位行列になってしまって掛けても実際は何も変わらないんですが、 この後似たような変換を繰り返すので、同じ形に合わせています。(こうしておくと、後で見やすくなるので)
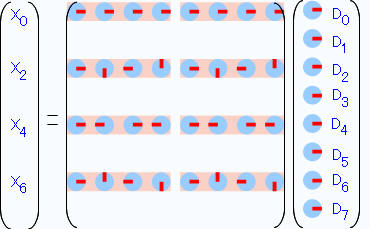
左右が同じ形の行列なので、さっき「あらためて行列について整理」の節でも触れたように、行列部分を「半分に変形」することが出来ます。
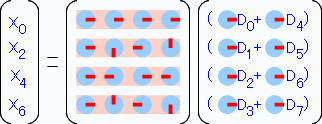
さて、同じように奇数の列についても共通部分を括り出せるか考えてみます。

先ほどの様に、行列の左右を見比べると、丁度反対向きになっていることがわかります。なので、上半分と下半分を同じ形にするために…
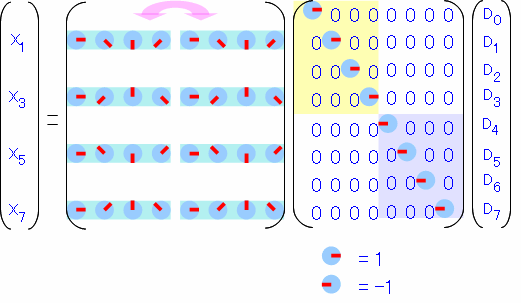
こんな風に上半分は「右矢印」を下半分は「左矢印」の回転因子を括り出すと、左右が同じ形になります。
この右側部分だけ先に計算してしまうと…

こうなります。行列の左右が等しいので、これも半分に変形することが出来ます。
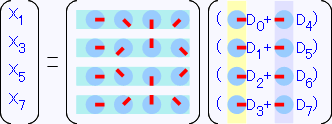
類似した部分を見つけ出すことで、8×8のDFT行列は、2つの4×4DFT行列にすることができました。 つまり8次から4次へと次数が半分になったわけです。
さらに分割してみる
8点DFTの計算は、2つの4点DFTに分割することができました。次数が下がったことによって指数関数的に計算量を削減できたわけですが、 さらに次数を下げることを考えてみます。
先ほどの2つに分けられた4点DFTの式を眺めてみます。
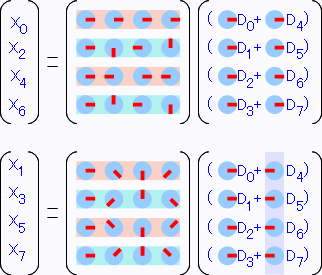
先ほどと同様に1行ごとにサーモンピンクと水色で色分けしました。これらの色毎に2つの式に分解してみます。
まずは上側からサーモンピンクの部分(X0、X4)を取り出したのがこれ↓。
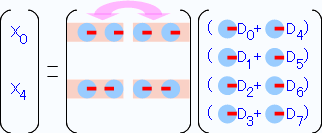
行列の左右を見比べると同じ形になっています。先ほどの様に共通項を括り出しておきます。(これも「右矢印(0度)」なので実質的には意味は無いのですが、 他と合わせる意味でこの様にします)
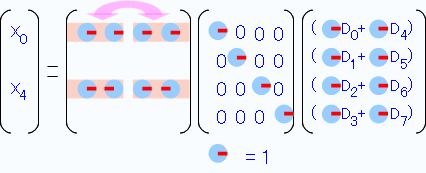
左右が同じなので、半分に変形します。
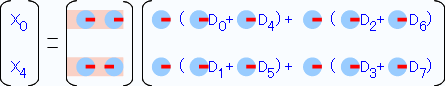
同じようにX2、X6のところも類似性を探してみます。
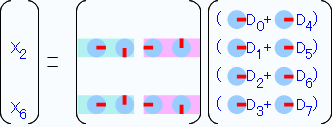
左右を比べると丁度反対向きになっているので、上半分(X2)と下半分(X6)それぞれから「右矢印(0度)」と「左矢印(-180度)」 を括り出します。
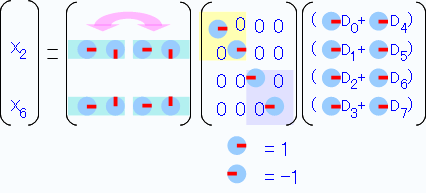
すると、行列の左右が同じになるので、半分に変形できます。
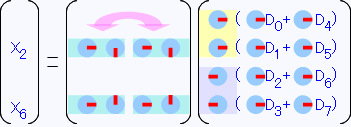
変形するとこうなります。
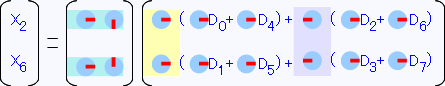
2つになった4点DFTのうち、偶数番(X0、X2、X4、X6)の方はこの様にさらに2つの2点DFTに分割することができました。
奇数のほうも見てみます。奇数のほうもやはりサーモンピンクの行と水色の行で2つに分けてみます。
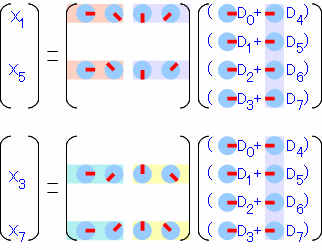
それぞれの行列を眺めて類似性を探してみます。X1、X5の方の行列は、右側を-90度回転すると左側と同じ形になることがわかります。 X3、X7の方は右側を+90度回転すると左側と同じ形になることがわかります。これらを括り出してみると、
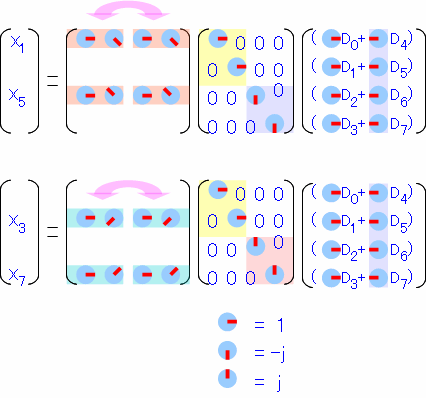
この様にそれぞれ左右が同じ形になります。右側の行列だけ先に計算し、さらに左右が同じ形なので半分に変形すると、
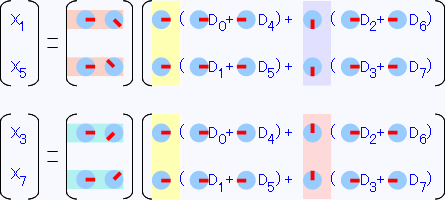
こうなりました。奇数番の方も2つの2点DFTに分割することができました。全部並べるとこうなります。
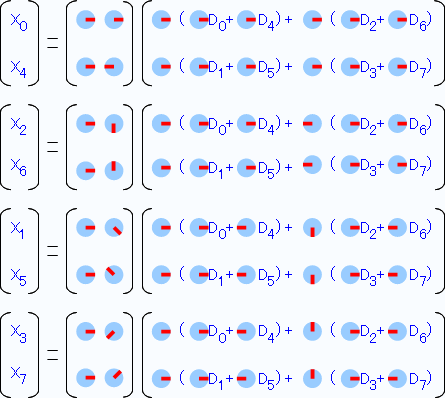
この様に、8点のDFTは4つの2点DFTに分割することができました。これらの式をもう少し実装に近い計算式に整理していきます。
バタフライ演算の図で表してみる
先ほどの式の行列を展開して、普通の方程式の形に直してみます。
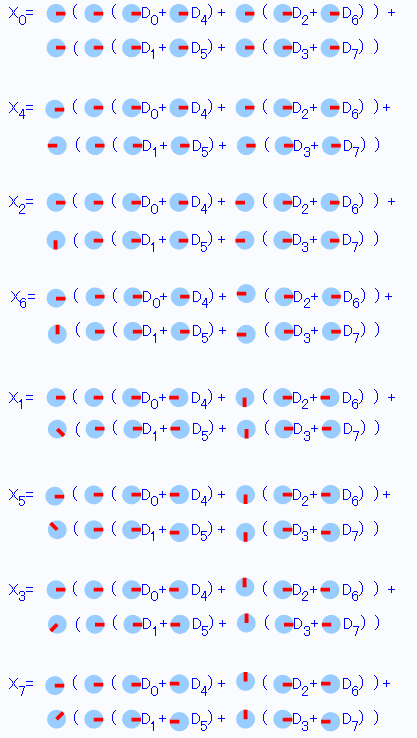
計算式の類似性を探す
これをX0からX7まで順に並べなおして、類似している部分に色を付けてみます。
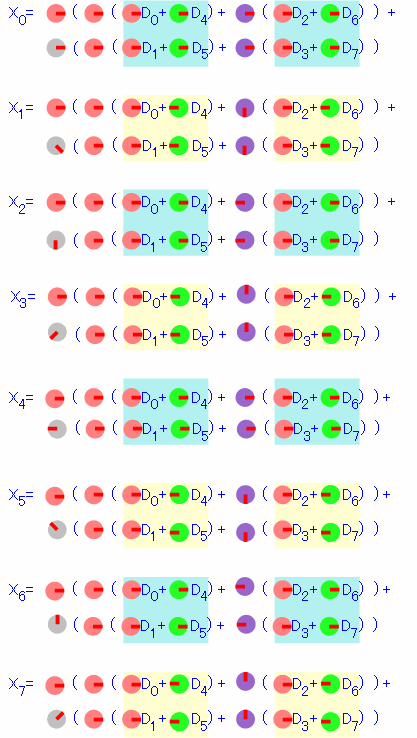
まず水色のところを見てみると、すべての式で同じ形をしていることがわかります。 これらは代表して1回だけ計算すればすべての計算時に流用することができます。 同様に、レモン色のところもすべての式で同じ形になっています。この計算も1回だけで済ますことができます。
ちなみに、緑色の矢印に着目すると、X0からX7に向けて半周(-180度)ずつ回転していると見ることができます。
紫色の丸に着目してみます。これはX0からX7に向けて-90度ずつ回転していると見ることができます。
さらに灰色の丸に着目してみます。これはX0から7に向けて-45度ずつ回転していると見ることができます。
シグナルフローグラフで表す
これらの規則性を元に、計算の流れをグラフィカルに表示する「シグナルフローグラフ」というもので表してみます。
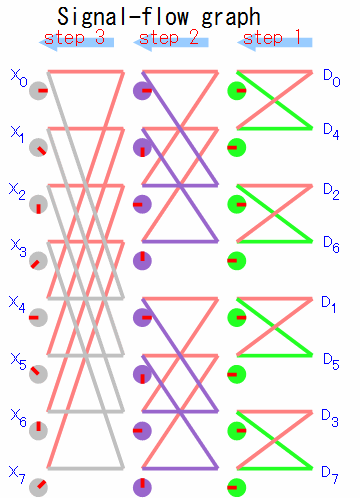
するとこの様に蝶々の羽がたくさん並んだ形が現れます。FFTのシグナルフローグラフはこのような形になるので、 「バタフライ演算」と呼ばれます。
バタフライ演算と先ほどの計算式を比べてみましょう。例えばX5だけ抜き出してみます。
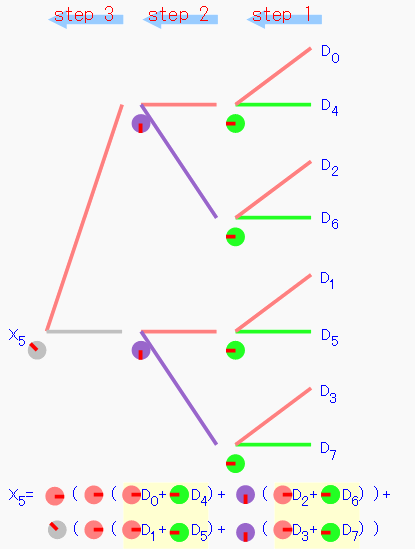
右側からの入力に対し、サーモンピンク色の線は「回転無し」、緑は-180度回転、紫は-90度回転、灰色は-225度回転して、 それぞれを足し合わせ、左に左に計算を吐き出して行って、最終的にX5が計算されることを表しています。 先ほどの式からX5を抜粋しました。確かに同じ計算を行っていることがわかります。
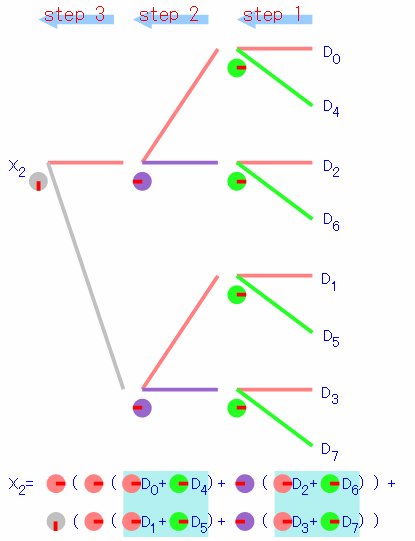
X2も見てみます。サーモンピンクと緑は回転無し、紫は-180度、灰色は-90度の回転を表しています。 先ほどの式と比べるとやはり同じ計算を表しています。
なお、一般的なシグナルフローグラフ(及びFFTのバタフライ演算のグラフ)は、計算過程が左から右に流れる様に描かれると思いますが、 このページではこれまでに挙げた行列の計算式と代入方向を合わせるために「右から左に」向かってフローが流れています。要注意。
さて、掛け算の数を数えてみましょう。
8点DFTの行列を展開する場合は、単純計算では8×8=64回の複素数掛け算が必要でした。 一方、バタフライ演算のグラフで掛け算に当たるのは緑、紫、灰色の丸印で、それぞれ丸印1個に付き1回の複素数掛け算が行われ、 8×3=24回ということになります。
実際は、さらに手を抜いて掛け算の回数を減らすことが出来るのですが、その前に「周波数間引き」という方法について触れておきます。





