ＰＩＣ　ＡＶＲ　工作室－＞ＴｏｐＰａｇｅ－＞資料倉庫－＞ＦＦＴ・複素数入門６

ＦＦＴの計算と複素数の入門６

FFT入門5からの続きです。

ビットリバーサルについて

ビットリバーサルとは

Cooley-Tukey型FFTでは、データを半分ずつに分けて入れ替えるという計算方法を繰り返すため、時間間引きでは入力データの並び順が、周波数間引きでは出力データの並び順がシャッフルされることになります。

このシャッフルされる順序は「ビットリバーサル」といって、データの順番値を2進数にしたものが、ビット順を左右鏡に映したように反転された値になります。8点FFTならこの様になります。（左が元の順序、右がビットリバーサルを行った後の順序）

時間間引きFFTではFFT処理を行う前にデータ列をビットリバーサル処理によってシャッフルしておく必要があり、周波数間引きFFTではFFT処理後にシャッフルしてから計算結果を参照する必要があります。

このビットが反転していく流れを見てみます。と言っても、例によって図で煙に巻きます。

時間間引きのビットリバーサル

まず時間間引きを見てみます。時間間引き8点FFTの8点から4点に分割していく計算の「途中式」を再度見直してみます。

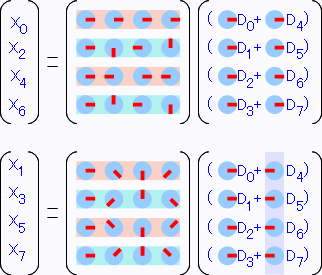
この右側を見てください。この様に入力データD0～D7が真ん中で2つに分割されて畳み込まれ、D0とD4、D1とD5という感じに並んでいます。以降も同じように半分、半分…とたたまれていきます。このような流れを図にするとこうなります。

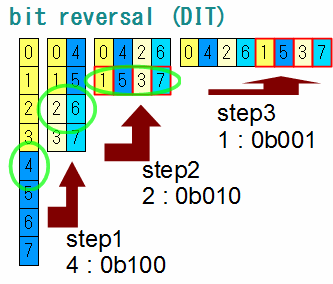
この図で注目する点は、まず一番左の緑の丸が付けられている「4」という部分。ちょうど半分に切った後半の先頭で、ここから切り取って右側に並べなおすわけですが、この「4」という数字は8点FFTならちょうど半分の値で、 2進数でいうと0b100となっています。

8点FFTではデータの並び順を2進数であらわすと0b000～0b111の8通りの数値が使われるわけですが、この0b100はこれらの中で最上位ビットだけが立った値です。左右反転すると0b001となって0の次に小さい値です。 step1でこの「4」が0の隣に降りてくるということに注目してください。

step2でさらに上半分を切り取って右につないでいく操作を行います。その先頭（緑の丸が付いてるところ）は2になっています。 2は2進数で0b010で、先ほどの4を半分にした値（1ビット分下がった値）になっています。

step3でさらに半分に切って右に繋ぎます。その先頭（緑の丸）は1になっています。1は2進数で0b001で、先ほどの2をさらに半分にした値（1ビット分下がった値）です。

このように、「4」（最上位ビットが立った0b100）が0の隣に並び、さらに半分、半分…となっていくごとに「2」（0b010）「1」（や0b001）が「より右のほう」に並ぶことになります。つまり節目の数値（4、2、1）は左が大きく右が小さくなるように並び変わったわけです。

またstep2で2と一緒に切り取って並べられる6というのは2と4のビット（0b010と0b100）両方が立った値になっていますが、この0b100は左右反転すると下位ビットに相当する部分です。step3で1と一緒に切り取って並べられる5や3や7も、（0b100、0b010）は左右反転した場合に（0b001）より下位のビットであり、それがうまいこと逆順に並ぶようになっています。

時間間引きFFTではこのような形でデータの並び順がクルクル入れ替わって、ビットの並び順が逆順になります。こんな風にして、データの並び順は2進数であらわしたビットの並び順が逆転する「ビットリバース」という順序に並び替えられるわけです。（数学的厳密性を無視した図なのでその点はいつもどおりご了承のほど）

周波数間引きのビットリバーサル

併せて周波数間引きの流れも見てみましょう。

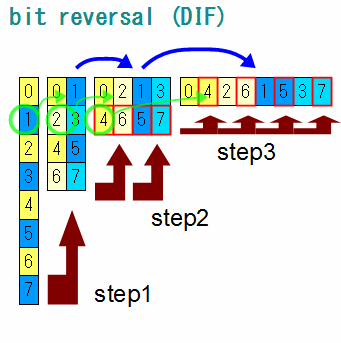
周波数間引きでは1個おきにデータを取り出して、それを順に右隣に並べていきます。ただし、さっきとはちょっとだけ右に並べていく動き方が異なります。

step1はそのまま青い箱の数字を右隣に移せばいいんですが、step2の「2」のところに付いている緑の丸は「0」の隣に移り、一方「3」は「1」の隣に移っています。こんな風に、1step毎に1列おきに隙間を空けてからそこに数字を移していくというような、ちょっとメンドい流れになっています。

「1」という数字の動きに着目してみます。step1ではまず0の隣に移動します。step2では「0」と「1」の間に1列挿入されるので、「1」は右に移動することになります。step3ではさらに2列挿入されるので「1」はさらに右に移動することになります。挿入されたところには「2」や「4」が入ってきます。この4とか2とか1というのは言うまでもなく先ほど同様節目の数字のことです。

節目の数字以外も同様にビット順がひっくり返るようにシャッフルされているのがわかります。

どちらの方式にしても同じようにビットの順序が同じ様にひっくり返ることが見て取れます。違うのは、FFT計算の前に行うのか後に行うのかの点。FFT計算前にビットリバーサルを行うのが時間間引き、後に行うのが周波数間引きです。

ビットリバーサルの実装については後述します。

実装時の検討事項など

これまで挙げてきたように、計算内容、処理方法を図で描き示すことが出来るということは、それを実装に落とし込むことはそれほど難しくはないはずです。例のexcelシートもこれまでの内容だけで書かれています。

しかし、実装では常に制約事項を加味する必要があります。 FFTを実装する上では、どのようなハードウェア（マイコン、PC、FPGA…）を使うのかによって、使用できる各リソースのコストは異なります。マイコンやPCならメモリ使用量はほとんど湯水のように使えるのにFPGAではメモリ使用量は節約が必要とか、 PCのメモリ構造はレジスタ→一次キャッシュ→二次キャッシュ→DRAM→HDDという順に遅くなるなど…環境によりいろいろな制約があり、リソース利用のコストは順位がまちまちです。

実装を行うにあたっては、それらの特性を加味しておく必要がでてくるでしょう。また、FFTの仕様そのものに関する制約もあるでしょう。そのあたりについて整理をしておきたいと思います。

FFTに入力するデータ数について

これまで8点FFTなどデータ点数が2のべき乗個となるFFTについて触れてきました。

しかし前にも触れましたが、FFTの入力データは2のべき乗個である必要は無いようです。これまでの例では基数（一番細かく分割するDFTのデータ数）が2となるFFTについて触れてきましたが、基数に3や4、5などを使うこともできるはずです。（計算式については触れませんが）

実際、そういう手を使う計算方法もあるようですし、半分、半分、半分…としていくよりも1/3、1/3、1/3… としていくほうが次数は早く収束していく気がします。また、サンプリング数のバリエーションという点でも2や3、5といった数値、さらにはそれらの組み合わせが使えると便利です。

このあたりは、実装の際の制約事項（処理時間？使用するメモリ量？プログラムのステップ数？デバッグやメンテナンスのしやすさ？など）に応じて最適と思えるものを探して選ぶことになるみたいです。詳しくは、「FFT　基数」などと検索してみてください。必ずしも2の指数乗である必要はありません。

（参考サイトの例）http://円周率.jp/method/fft/radix.html

開発基盤と制約、処理効率について

例のEXCELシートで、0度や-180度の回転について「加減算」に置き換えずに「sinやcosの計算式」を用いるようにしているのは、基数とはまた別の「実装面の制約事項」を加味してのものです。

→私の場合、EXCELシートを作った後、この計算ロジックをそのまま応用してAVRのAT-MEGA用にアセンブラでフルスクラッチしようと思ったのですが、その際に、0度と-180度だけ特殊処理にするとなると分岐処理が必要になってしまい、返ってプログラムは長く複雑になってバグを作りこみそうだし、一方データ長を8ビットの整数型で処理させるつもりなので、実際の掛け算処理自体はCPU内蔵のハードウェア乗算モジュールでサクッと（2クロック×2回（実数＋虚数）=4クロック＋α）できてしまう算段も立っていたので、あえて掛け算をしてしまっても処理時間にほとんど悪影響はないだろうと踏んで、 EXCELシート上もそのような計算処理としました。

というわけで例のEXCELシートの計算式を眺めると、例えば8点FFTは掛け算数が「10回」ではなく「24回」に相当する計算式を組んでいます。

現実的には、どんな処理環境でどんな制約を満たす必要があって、どんなパラメタは劣後していいのかといった優先順位を加味した上で、どんなFFT計算処理を組むのが似つかわしいのか考えていく必要があるようです。

PCのような複雑な仕組みのCPU（MPU）では、CPUレジスタやキャッシュRAM内でメモリアクセスが済んでしまうほうがメモリI/Oが速くすむので、 DRAMへのアクセスを極力させずない様に見越したロジックで組むということも行われていたり、 FPGAなどではRAMやROMにあたる回路を組むと無駄にリソースを消費してしまうので避けるなどの考慮も行われる様です。まぁ、「万能なものはない」ということでしょう。

逆に、制約があまりきつくないのであれば、汎用的なFFTライブラリを使っても特に支障はないでしょう。

FFT計算値のレンジについて

FFTの計算を行う場合、例えば8点FFTの入力データとして「1」を8個（＝直流成分）与えてみると、 FFTの結果は直流成分に「8」という元の8倍の値が抽出されます。「1」ではなく「8」となることに留意。

なお、直流以外の周波数についても同様に8点FFTなら8倍、64点FFTなら64倍となりますが、これらは「正の周波数」と「負の周波数」にそれぞれ分かれて抽出されるため、それぞれ4倍、32倍の値が正／負それぞれの周波数に抽出されることになります。

さて、このような値は浮動小数点演算によるFFTなら問題なく扱うことができますが、言語仕様として浮動小数点が扱えないアセンブラの様な場合や、高級言語であっても「計算精度」より「速度」を優先するために整数型の変数を用いたいというケースもあるでしょう。

この様に整数型変数の場合に注意が必要なのは、FFTの各STEPの計算を行うごとに、変数に蓄えられる数値のレンジが最悪「倍→倍→倍…」と増加していく可能性があるということです（基数2のFFTの場合）。つまりFFTの処理を1stepずつ重ねていくたびに格納する変数のビット幅が1ずつ増えていくということです。 8点FFT（8=2^3）なら3ビット分、1024点FFT（2^10=1024）なら10ビット分増えるわけです。浮動小数表示なら指数部が変化していくだけですが、整数型の場合は「固定小数点変数」の一種なので、 1step計算するごとに入れ物の大きさを1ビットずつ増やす必要性があるわけです。

そして可能性があるということは当然それに備えて入れ物（＝変数）のレンジもそれに見合う大きさにしておく必要があるということです。変数（やアセンブラならレジスタ）のビット幅が入力データの幅に対してギリギリのデータが格納されているとしたら、 FFTの1step分の計算を行ったとたんに桁あふれが生じてしまう可能性が生じます。例えば16ビット型配列の各変数に-32767～32767ギリギリいっぱいのレンジ（※１）のデータが格納されている場合、 1step目でいきなりあふれる可能性があります。

特に、バタフライ演算の「回転因子の掛け算」部分ではなく、足し算や引き算の部分であふれます。

このような場合、一旦1step分のバタフライ演算を16ビット幅+キャリーフラグ1ビット=17ビット幅で行っておいてから、各配列に書き戻す時（※２）にこの値を半分にする（キャリーも含めて1ビット右シフトにより半分を計算）ことで、常に16ビット幅の変数に収めることが可能になります。

最下位ビットを毎step捨てていくので計算精度が多少下がるのと、本来のFFTの値のようなデータ点数倍（8点FFTなら8倍）の値ではなく「1倍の値」として抽出されるのですが、周波数毎のスペクトル成分の量を「大小の情報」として抽出するだけの目的（オーディオのグライコのような用途）では、特段支障はないでしょう。

計算数値のレンジや精度を必要とするFFTの場合は多ビットの浮動小数点変数で、速度を優先するのであれば固定小数の整数型といった具合にデータ型を選択することも設計／実装の際に検討が必要になるかと思います。

※１：-32768は引き算すると+32768となって16ビット変数で表せなくなるので使用できない。

※２：Cooley-Tukey型FFTでは、バタフライ演算で計算した値は各stepで別々に格納しておく必要は無く、元の変数に上書きして戻しておき、次のstepでまた読み出して使用する。このような計算方法をIn-Placeといい、代わりにビットリバーサル処理が必要になる。ビットリバーサル処理が必要ないFFTロジックもあるがOut-Placeとなる。

ビットリバーサル処理の実装について

Cooley-Tukey型FFTではビットリバーサルの処理が必要になるのですが、ソフトウェアで実現しようとすると簡単な数値計算だけでは済まないので少々面倒だし、計算時間もかかります。一部のプロセッサではこのようなビット反転を行う計算がCPUネイティブ命令で用意されているようですが、普通は用意されていないと考えた方がよさそうです。

ソフトウェアFFTでは、あらかじめビット入れ替えを行うための変換テーブルを用意しておいて、テーブルサーチ（と言っても配列の添え字による参照）で入れ替え先を求めるというのが一般的でしょう。処理時間が短くて済み、簡単です。デメリットとしては、メモリ上に変換テーブルを置いておく必要があるということになりますが、必要となるメモリ量はたいしたこと無いので、あまり気にする必要は無いでしょう。

一方、FPGAなどHDLを使ってビット反転するのは簡単ですね。単純にビット列のオーダーを入れ替えるだけで済んでしまいます。

窓関数について

FFT（またはDFT）を掛けるとき、入力信号の成分がきりのいい周波数だけで構成されている場合は特に問題がないのですが、現実はそれほど都合がよくありません。

例えば、64点FFTを掛けるときのことをシミュレートしてみます。サンプリング周波数を6400Hzとして64点FFTを実行してみると、成分を抽出できる最大周波数（ナイキスト周波数）は3200Hz、分解能は100Hzとなります。

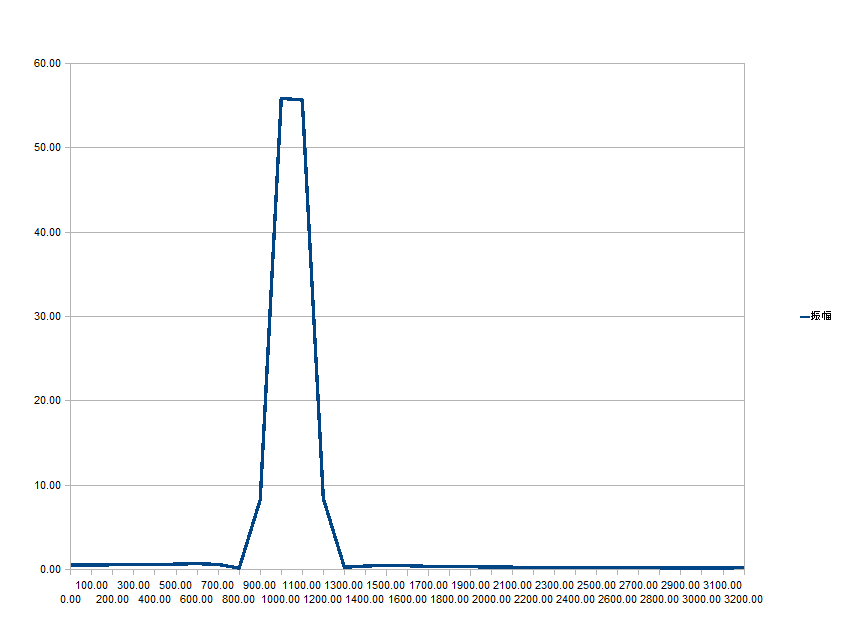
100Hz単位なので、1000Hzとか1100Hzの様にきりのいい周波数が入力された場合は問題ないんですが、自然界の波形はそんなに都合のいい周波数ばかりではありません。例えば、ちょっと中途半端な1050Hzという信号をFFT掛けてスペクトルを見てみると…

こんな波形になります。

確かに1000Hzと1100HZあたりにピークがありますが、山の裾野のような曲線も周囲に載っていることがわかります。 DFTやFFTは、ある一定区間の信号を取り出して、それが延々と連続しているということを前提にして計算処理を行います。ところが1050Hzという信号を入力すると64点分でちょうど１周とはならないので、信号の頭とお尻がきれいに繋がらず（不連続）、あたかも「ノコギリ波」などが混在した波形という風に解釈されてしまうようです。

「各周波数成分毎のスペクトルを知りたい」という用途の場合、このように幅広く成分が拡散してしまうと都合がよくありません。このような場合、1000Hzと1100Hzの2つに分かれて抽出されるとうれしい訳です。そんなことができるなら問題は一気に解決なわけですが、まぁ想像通り解決策はあります。

そのためには、周波数の近い波と波を重ねると「うねり」というものが生じることを考えると「あっ、それね！」となるのではないかと思います。例えばこんなグラフ。緑色の線に注目。

詳説はしませんが、こういうのを実現するために「窓関数」というのを使うとうまい具合に両端が繋がり、かつ目的の1050Hzの両側の周波数（1000Hzと1100Hz）として抽出できることが想像できるでしょう。

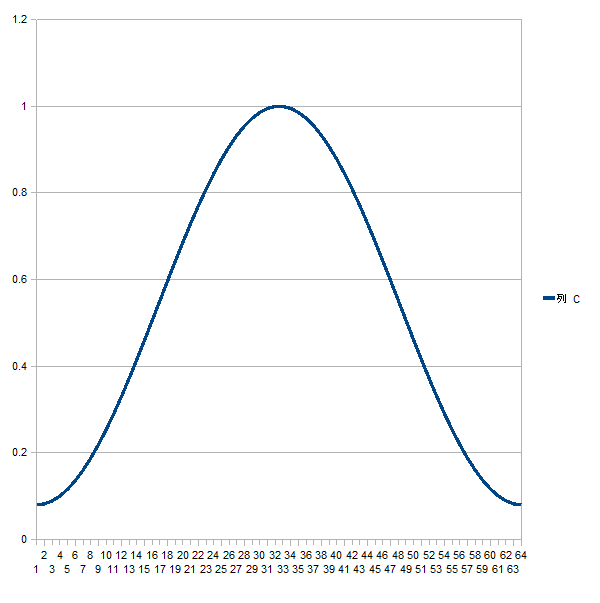
窓関数にはいろいろな種類があって、それぞれ特性がことなります。よく使われるものの中に「ハミング窓（hamming window）」というのがあります。ハミング窓というのはこんなグラフを描く関数です。

入力信号（1050Hz）に対しこのハミング窓関数を掛けてからFFTを掛けるとどのようになるか見てみましょう。

このように、ほぼ1000Hzと1100Hzに分かれて抽出されることがわかります。ただし、よく見ると900Hzとか1200Hzのところにも少し成分が載っていることが見て取れます。

さらには1000Hzのようなきりのいい周波数の信号を入力した場合でも、窓関数を通してFFTを掛けると実は1000Hzだけでなくその両側(900Hz、1100Hz）にも周波数成分が散ってしまいます。

このように、「窓関数」を掛けると抽出できる周波数は若干ぼやけてしまいます（周波数分解能が悪化）。窓関数にどんな関数を使用するかによって周波数分解能やその他の性能に差が出ます。どんなアプリケーションを実現したいのかによって使用する窓関数を選択する必要があるようです。

また、窓関数は入力信号の両端の信号の一部分を削り落とす計算処理でもあるので、窓関数＋FFTで求まった値の持つエネルギー量は、元の信号が持っていたエネルギー量よりも少なくなります。アプリケーションによってはこの点を注意しておく必要があるでしょう。

「ハミング窓」について紹介しましたが、他にどのような窓関数が存在して、どのように計算し、それぞれどのような特性があるのかは、wikipediaなどをご参照ください。

レスポンス時間と周波数分解能について

DFTの代わりにFFTの計算ロジックを用いれば、どのような動作環境であれFFTの方が短い時間で処理を終えることが可能でしょう。そして同じ計算ロジックでも「より速い」プロセッサを用いれば極めて短い時間で処理することができるのは言うまでもないでしょう。

ただしこの「計算時間」というのは、入力データが全部そろってFFTの計算処理を開始してから計算結果が出るまでの時間のことです。この部分は確かに短くできますが、FFT計算を行ううえで短くするのが根本的に困難な部分も存在します。

それは「全データをサンプリングし終える時間」です。データが無ければFFTがはじめられません。リアルタイム処理としてFFT計算をする場合、必要な全データのサンプリング完了までの時間は避けられないタイムラグになります。

FFTの計算には、8点FFTなら8個の、32点FFTなら32個の入力データが必要になります。リアルタイムでFFT計算を行うと言ってもそれぞれ8個、32個といったデータを「一定の間隔ごとにサンプリング」してからFFT計算の処理が始まります。（図は8点FFTを行う場合のADCからのサンプリング時間と、FFT演算処理をあわせた時間のイメージ）

仮にADCからサンプリング周波数＝20000sps（samples per second…この場合ナイキスト周波数は20000÷2＝10000Hz）でサンプリングを行い、 32点FFTを掛けると仮定します。データ1個をサンプルする所要時間は1/20000sなので、32個では32/20000s（＝1/625s）を要します。一般化すれば、周波数分解能は以下の式で表されます。

「周波数分解能　＝　サンプリング周波数　÷　データ点数」　または

「全サンプリング時間　＝　データ点数　÷　サンプリング周波数」

どんなに速いプロセッサと計算ロジックを使っても、20000spsで32点全データならサンプリングを終えるまで固定で1/625秒を要し、それより早くFFTを完了することはできないわけです。というか、計算を開始することが出来ないわけです。

ADCからのサンプリングデータが128点、512点、4096点のように増えれば増えるほど、それに比例して時間も長くなります。この時間は当然「タイムラグ」となります。全データのサンプリングを完了するより早くFFT計算を終えることは不可能なわけです。

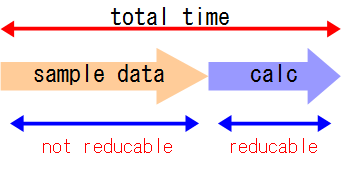
一方もし32個よりも少ない点数でFFTを行えば、当然この時間は1/625秒より短くすることができます。しかしその場合、分離可能な周波数の最小単位（周波数分解能）が悪化してしまいます。 20000spsで32点FFTを行う場合周波数分解能は20000÷32＝625Hzですが、仮に16点FFTに減らせば1250Hzに、 8点FFTにすれば2500Hzに低下してしまいます。これら以下の周波数成分には分離把握することはできません。

このように周波数分解能とレスポンス時間は「二律背反」の関係にあります。

ちょっと待て、と。データ点数を増やすことで劣化した周波数分解能の分を補うために、サンプリング周波数自体を上げてしまえば（例えば40000spsとか80000spsとか）いいじゃないか、と考えたくなります。

でもそうしてしまうと、周波数分解能は「サンプリング周波数÷データ点数」ですから、仮にデータ点数を2倍に増やし、サンプリング周波数も2倍にあげると…全データサンプリング終了までの時間は確かに長くはなっていませんが、周波数分解能も元のまま変わりません。（がんばった分は、高域の周波数を拾うことに寄与しますが、周波数分解能の向上には寄与しません）

整理します。細かい周波数分解能で各周波数の成分を把握したいのであれば分母を大きく取る（FFTに入力するデータ点数をたくさん確保する）必要があるけどレスポンスは悪化します。一方で分母を小さくする（データ点数を減らす）とレスポンスは向上しますが分解能は低下します。またある周波数分解能を実現するためには、全データのサンプリングが完了するまでに一定の時間が「絶対的」に必要になり、 FFT完了までの時間はその全サンプリング時間よりも短くすることができない、ということになります。

音声データなどをリアルタイム処理する場合には、このような周波数分解能とレスポンス時間のバランスをどのように設定するかということが、アプリケーションを実現する上で重要な検討ポイントのひとつになると思います。

レスポンス時間と周波数分解能についてもうちょっと

なお現実的なことについてちょっと触れておきます。例えば32点FFTの場合、本当に32個のデータ全部がそろわないと周波数成分が眺められないかというと、経験則的にはそうでもありません。

例えば32個のうち半分（16個程度）のデータが集まった状態（残りのデータは「0」と仮定）でFFTの計算を行ってみると、 32個全部の時の計算結果と比べて、データが持つ周波数成分と比較すると確かに一部分しか抽出されていないという内容になるのですが、逆に言えば一部分だけは目的の周波数成分が抽出・把握できるようです。データ数を少しずつ増やしていくと徐々に目的の周波数成分が増えていく様子が見て取れます。ただし、その場合はピーク周波数以外のところにも裾野の様に成分が載るので、計算値の取り扱いは必要でしょう。

レスポンス時間も周波数分解能もどちらも制約事項が厳しいと言うようなアプリケーションの場合は、このような「サンプリング途中」でその該当成分がどのように抽出されていくのかという変化過程の視点は大事になるのではないかと思います。

具体的にどのような場合にどのように抽出されるのかを理論的に記すのは難しいので省きますが、例のexcelシートに「一部分だけのデータがADCからサンプリングできた」と仮定してみたときに、 FFT結果にどのように抽出されるのかを眺めてみると面白いと思います。→例のexcelシートで「ハミング窓」を掛けてから実験してみてください。（サンプリング済みのデータが1/3とか半分とかで残りのデータは「0」と仮定し、そこからサンプリング済みデータが少しずつ増やしていくようにシミュレーションしてみると、該当周波数の成分が徐々に増えていく様子が見えると思います）

なお、ギターシンセ（エレキギターのピックアップ機構などからアナログ信号を入力し、それをMIDI信号出力に変換→MIDI音源から好きな音色で音を鳴らすというもの）のようなアプリケーションでは、タイミングはとてもシビアでありながら、一方で弦の振動数（周波数）や弾いた強さ（振幅）の情報についてもシビアな分解能が求められることになります。

一般に、ギターシンセではこのようなFFTの代わりに周波数－電圧変換回路（FVC）を用いたり、さらにピックで弾く動作を別の手段も併せて検知するなどしてレスポンス確保の工夫をしているようです。

信号から周波数成分を抽出して利用する場合、その方式としてFFT以外にも存在するということを念頭においておく必要があるでしょう。仮にマイコンを使った工作などで、ある特定の周波数（1つの特定の周波数、もしくは数個程度）を検知したいという場合、トーンデテクタというタイプのIC（例：NE567）を使えば簡単な回路で検知することができ、FFTは使う必要ないわけです。

周波数を検知するというアプリケーションを実現するだけでも、FFT、FVC、トーンデテクタ…実現方法はいくらでもあるわけで、レスポンス時間と周波数分解能の観点だけでもいくつかのソリューションの中からアプリケーションに最適なものを選べばいいわけです。

回転因子テーブル

FFT（DFTも同様）の計算を行う際、回転因子による回転計算を大量に行う必要があります。回転因子は一般に複素数の形で表します。極座標表示であれば長さは「1」固定、角度はグルグルいろいろなバリエーションとなるわけですが、どんな処理言語でも極座標表示による複素数型演算機能が実装されているとは限りません。一般的な処理言語系では極座標表示による複素数の演算機能は実装されていないことが多いでしょう。

一般的な処理言語系で回転因子による「回転計算」を行うには、オイラーの公式を使って複素数を直交座標系の「実数軸」と「虚数軸」に分けて、実数部、虚数部を「別々の実数変数」にて扱うことになると思います。しかもそれを高速に効率よく行うためにはいちいち三角関数計算を行うわけにもいきません。処理速度を考えれば、回転因子で必要になる三角関数の「値」を事前に求めておいて、それを定数テーブル化しておくのが普通の考え方でしょう。

では、どのような定数テーブルを作ればよいのでしょうか？

バタフライ演算の図を見返してみます。

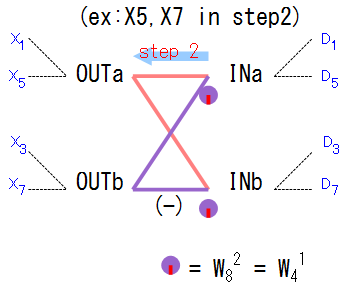
バタフライ演算を１個取り出してみると、「線」の数、つまり４つの演算が表れることがわかります。そのうち2つは「複素数同士の足し算」なのでテーブル化とは無縁です。残りの2つは、片方は回転因子を掛けて足し、もうひとつは回転因子を掛けて引くという複素数計算をします。テーブルを用意しておく必要があるのは当然この回転因子1個1個です。

そして、すでに触れたように回転因子による回転は、「0度」と「-180度」の回転計算を掛け算のまま行ったほうが楽か、足し算引き算に置き換えた方が楽なのかというのは開発基盤によって異なることが多いでしょう。しかし、掛け算（回転）に用いる回転因子は0度～-180度までとするのか、それとも-180度～-360度も含めるのかという点については考えるまでもないでしょう。（アセンブラレベルに展開すれば）足し算と引き算は処理速度で考えれば一緒のはずです。という点を加味し、テーブルには0度～-180度だけ用意しておき、 -180度～-360度は引き算に置き換えてしまえばテーブルデータは半分に減らすことができます。しかもこの場合のデメリットは特に無いでしょう。

ちなみに例のexcelシートについても、三角関数の掛け算は0度～-180度までで計算し、 -180度～-360度の計算は0度～-180度の引き算によって行っています。つまり、「1周分の半分の回転因子」についてテーブル化しておけばよいわけです。

さて、もう一つの視点。

例えば64点周波数間引きFFTでは、1step目では64点DFT用の回転因子（の0度～-180度の範囲のもので計32個）が、 2step目では32点DFT用が、3step目では16点DFT用が…となることについて触れました。

この2step目以降で使用する回転因子について考えてみます。

64点DFTで使用する回転因子の最小単位をW64とすると、1step目の回転因子テーブルはこのW64のべき乗（0乗～31乗の32個）で求めることができます。2step目はというと、32点DFT用の回転因子テーブルW32のべき乗（16個）、 3step目ではW16のべき乗（8個）…を用意することになると想像できます。

ただし、32点DFT用の回転因子は64点用のものを「2乗したもの（指数部が2倍になったもの）」で代用することができることから便宜上32点DFT用の回転因子を用いているわけで、別に64点DFT用回転因子を（一つ飛ばしで参照するように）使っても計算できないわけではありません。むしろメモリ使用効率から考えれば、一つのテーブルで代用できるのであればその方が効率的ともいえます。

ではなぜstepが進むにつれて「データ点数が半分のDFT用回転因子テーブル」をわざわざ用意して使うのか？？？

細かい話になりますが、多分高級言語レベルで考えればどちらでもいいという気がします。ただ、高級言語でコーディングしてもアセンブラでコーディングしても、どちらにしても最終的には機械語として実行されます。そのときに、回転因子テーブルを舐めていく処理で一つ一つ「インクリメント」することも想像できます。 C言語で言うとfor文の増分指定が「i++」のような形なのか、「i=i+4」のような形になるのか、といった話です。

その際に、機械語レベルでただインクリメントするのと、2とか4とか8とかを足しこんでいくことを比較すると、当然前者のほうが処理時間は短くて済むでしょう。多分このような機械語レベルに翻訳した際の処理時間を加味して複数のテーブルを持つのが一般的になっているものと思いますが、実際はどっちで計算してもそれほど大きな差にはならないような気がします。（ロジック次第）

というわけで、step毎に回転因子テーブルを分けても、一つの回転因子テーブルを使いまわししても、処理速度的にはあまり影響はないと思いますが、むしろ処理方法の考え方としてはstep毎に別々にしたほうがシンプルで解りやすいロジックになる気がします（特にソフトウェアで実現する場合）。

FPGAなどHDLでは、テーブル回路にする場合と計算ロジックにする場合で使用メモリリソースをどちらが節約できるのか考えて選択する必要があるのだろうと思います。

その他

偶関数、奇関数という概念があります（詳しくは触れませんが）。これらを利用すると、FFTの入力データには実数部に1組のADCデータ、虚数部にもう1組のADCデータをセットしてFFTを行い、その計算結果から2組それぞれのFFT結果に分離することが可能だったりします。

つまり同時並行的に2組（またはそれ以上）のデータをFFT掛けるアプリケーションでは、この方法を用いると「単純計算でほぼ倍」の計算速度を得ることができます。計算方法などには触れませんが、「FFT 2組同時」などと検索してみてください。

その他にも、計算時間を短く済ます方法などがいろいろ編み出されているようなので、調べてみるとよいかもしれません。

DFTとFFTの簡単なまとめ

改めてDFTとFFTを勉強しなおしてみて気づいたことなどを纏めておきたいと思います。

DFTについて

学生時代からずっとFFTを避けてきた最大の理由は、複数の重ね合わせた波が「なぜ一つ一つの波に分離」できるんだろう？これってオカルトじゃないの？と思っていたため。1+2は3だけど、3は1+2なのか、1.5+1.5なのか判らないはずなのに…と。

これに関するブレイクスルーは、元となるサンプリングデータをn次元のベクトルとしてあらわし、それと各周波数毎に設けた単位ベクトル（回転因子行列の横1行分）との内積を計算することによって「類似性」を計算し、類似性を各周波数成分（及び位相）として抽出することでした。波の重ね合わせは単なる足し算ではなく「合成」であり、合成した波から各周波数成分を抽出するのは単なる引き算ではなく類似した周波数を抽出する「分離」の計算。

一方、複素数がなぜ登場するのか。これは回転計算を束ねてたくさん行うときに便利な「ツール」と割り切ること、およびオイラーの公式を用いることで直交座標表示と極座標表示が簡単に変換できることなどを考えれば手間を省くことにつながります。 FFTの行列計算（回転因子行列による変換）はあたかも実数の代数演算のように計算できて楽チンになるので、利用価値が高いことが改めて理解できるわけです。

で、これら「サンプリングしたn次元ベクトルと回転因子との内積（行列計算）」と「複素数による回転計算」という概念を用いると、あの難しそうに見えたDFTの計算は「簡単な行列の計算」で表現できることがわかりました。DFT、恐れるに足らずです。

FFTについて

DFTが解ってしまえば、あとは如何に手を抜いて計算するのかという話になるわけですが、ここでもやはり複素数による回転計算を用いることで、計算式が体感的に解りやすく扱うことができました。（もし実数のsin、cosだけ使って計算したら面倒で死んでしまうでしょう）

「複素数による回転」を加味して回転因子行列の中の「規則性」を見つけやすくすることで、 DFTの行列はn次元から小さく小さく切り刻んで次元数を順次下げることができ、小さい次元のDFT（特に当サイトでは半分・半分…と基数＝2のDFTまで切り刻みました）に分離することで高速に計算できることまで確認できました。

計算結果の見方について

時間間引きと周波数間引きでは、ぞれぞれFFTの計算前・計算後にビットリバーサル処理を行う必要があることに触れました。ビットリバーサルを行わないと順序が狂ってしまうわけです。（※：ビットリバーサルが不要なFFT計算方法もあります）

そのFFT計算結果の見方について。n点DFTでは「0番目」の結果が直流、それ以降は「サンプリング周波数/n」毎に抽出された成分が順々に格納されていて、「n/2番目」のとき（例えば64点FFTでは32番目）に最高周波数（ナイキスト周波数）となり、ナイキスト周波数ではcos成分しか抽出できないことについて触れました。さらに「n/2+1番目～n-1番目」は負の周波数として抽出されることについて触れました。

このときの「サンプリング周波数/n」は周波数分解能で、これより細かい周波数には分離ができないということもわかりました。

一方、入力データには「窓関数」を掛けるとによって周波数分解能の整数倍の周波数に限らず、その中間の”自然な周波数”についても目的の周波数成分として抽出することができることがわかりました。ただし、窓関数を使った場合は周波数分解能が少しぼやけてしまうことがわかりました。

そしてこのような「周波数分解能」と「レスポンス時間」は二律背反であることについて触れました。

これらのようなことを念頭に設計をすれば、どのような実装をすればアプリケーションの目的に対してもっとも「合目的」的なのかが明確にできるでしょう

感想など

改めて今になってFFTの勉強をしてみようと思ったのは、マイコンのADCから取り込んだ音声データから周波数成分を抽出し、 MIDI楽器の入力部分（具体的には弦楽器を元にしたMIDIマスター）の機能を実現したいと思ったからでした。

弦楽器的なMIDIマスターの例としては、先述のようにギターシンセというものがすでに販売されていて、 FVCという仕組み（とその欠点を元に改善したもの）を利用しています。私も似たようなものを作りたいと思ったのですが、あくまで趣味レベルで作りたいのと、ピックアップ回路周りからギターシンセとはずいぶん違ってたりもするので、一からオリジナルで作ろうと。で、部品は入手しやすい汎用品レベル（入手しやすいマイコンなど）で済ませ、周波数成分の抽出も極力ソフトウェアで済ませてしまおうと思い、学生時代以来避けてきたFFTに改めて手を出してみました。

各種言語用、もしくは各種マイコン専用のFFTライブラリはすでにたくさん公開されているので、周波数の抽出を手っ取り早く済ますならこういったライブラリを使うのが一番楽なんだと思います。しかし、このようなライブラリを使用することを考えたときに、2つほど気になることがありました。

一つは、これらのライブラリは比較的汎用用途の仕様になっていて、楽器に使うにはレスポンスや精度について自由に調整できないという点。弦楽器であれば弾いたときの音量、音の鳴りはじめと音が止まるときのレスポンスが重要。少しでもいいから要件にフィットするように調整したいと思っても、ライブラリの仕様がブラックボックス状態では弄りようがありません。

もう一つは、何か思わぬ結果になったときに転んでも泣かないため。 FFT計算処理で出力される数値の見方…特に複素数の何たるすら解らなかった状態だったので、複素数FFTのライブラリを使用してもその計算結果がナニを示すのか、そもそも正しい結果が出ているのかも検証できないし、計算結果からどのようなタイミングでどのような情報が抽出できるのか？といったこともよく理解できておらず。せめてFFTのイロハのイくらいは理解しておかないと、と。

で、例の本をじっくり読んで、ようやく複素数とFFTの何たるかがつかめてきたという感じです。解ってみれば「なるほど」と思えるもので理論的には筋の通った話だったし、なによりいろんなことに応用が利くものなので、どうせなら各アプリケーションに沿ったライブラリを自分で作れる位のことを整理しておきたい、と思ったわけです。

（FFTに限らず、当サイトの他のページを見ていただいても判りますが、基本的に誰かに情報を解説したり伝えたりするためのサイトではなく、自分で理解したことを文字や図に表してみることで、そもそも「本当に理解できているのかどうか」を自分自身が確認することがのこのサイトの目的だったりします。 …アタマにインプットするだけでなく、アウトプットの過程を通じて「理解度を確認」「勘違いを正す」のが目的、サイト自体はその過程の成果物）

とりあえずDFTやFFTについては自分自身が知らなかったこと、疑問に思ったことについてそれなりに調べてみたつもりです。が、あまりアカデミックなこと自体には関心がないので、理論的厳密性は「当然のように無視」しています。一方、数学的センスのない私がさらっと読み返してみた時に、ウソが本当のように書いてあるということは無いように心がけたつもりではありますが…

というわけで、個人的にはなんとなくFFTの計算を行うイロハは解った気がしますが、もし間違えなどあったらこっそり伝えていただけるとうれしいです。

とりあえず、FFTとは何ぞやとか、複素数が何故FFTで使われるのかとか、どんな風に計算してどんな風に計算値を解釈すればいいのかなどについて自分なりに理解できた気がするので、 FFTについてはひとまずこれで締めたいとおもいます。